2 机器学习基本概念

可先阅读，也可在后续章节用到时返回来阅读。

分类评估指标

1. 阈值依赖的指标 (Threshold-dependent): 包括准确率 (Accuracy)、精准率 (Precision)、灵敏度 (Sensitivity)、F1得分。这些指标都依赖于一个固定阈值界定的混淆矩阵 (confusion matrix)。通常这个固定阈值为0.5，采用服从多数原则。 但这对不平衡样品是不合适的。

2. 阈值不依赖的指标 (Threshold-invariant): ROC曲线，定义了在一系列分类阈值空间上真阳性率与假阳性率的变化关系。This includes metrics like area under the ROC curve (AUC), which quantifies true positive rate as a function of false positive rate for a variety of classification thresholds. Another way to interpret this metric is the probability that a random positive instance will have a higher estimated probability than a random negative instance.

2.1 分类问题模型评估指标 - ROC曲线和AUC值

分类问题评估指标有：准确率 (Accuracy)、精准率 (Precision)、灵敏度 (Sensitivity)、ROC曲线、AUC值。

假设有下面一个分类效果评估矩阵Confusion matrix (也称混淆矩阵，总觉得这个名字奇怪，或者成为预测错误矩阵)，如下：

行代表实际值，列代表预测值。如DLBCL组有56+2个样品，其中56个被预测为DLBCL，2个被预测为FL。

confusion <- data.frame(Predicted_as_DLBCL=c(56,8), Predicted_as_FL=c(2,11), 
                        class.error=c(0.03448, 0.4211),
                        row.names = c("Originally_classified_as_DLBCL",
                                      "Originally_classified_as_FL"))

confusion

##                                Predicted_as_DLBCL Predicted_as_FL class.error
## Originally_classified_as_DLBCL                 56               2     0.03448
## Originally_classified_as_FL                     8              11     0.42110

2.1.1 准确率 (Accuracy)表示预测正确的结果占总样本的比例

计算如下：

\[ 准确率 = \frac{56+11}{56+2+8+11} = 0.870 \]

准确率可以判断总的正确率，但在各个分组样本数目差别较大时不能作为一个很好的评价标准。比如上面confusion matrix中，所有样品全部预测为DLBCL时准确率可达75.3%。这一不负责任的预测方式 (也称为No information rate)跟预测模型的准确率 (87.0%)相差不是太大。

2.1.2 精准率 (Precision)

• 所有被预测为DLBCL的样品中有多少确实是DLBCL;
• 所有被预测为FL的样品中有多少确实是FL;

\[\begin{align} 精准率(DLBCL) &= \frac{56}{56+8} = 0.875 \\ 精准率(FL) &= \frac{11}{11+2} = 0.846 \end{align}\]

2.1.3 召回率 (recall)

灵敏度 (Sensitivity)/召回率 (recall)也称为真阳性率。

• 实际为DLBCL的样品中有多少被预测为DLBCL；
• 实际为FL的样品中有多少被预测为FL:

\[\begin{align} 召回率(DLBCL) &= \frac{56}{56+2} = 0.966 \\ 召回率(FL) &= \frac{11}{11+8} = 0.579 \end{align}\]

不同的分组，召回率(Sensitivity)值差别很大，尤其是样本数目不均衡时。

2.1.4 假阳性率 (false-positive)

假阳性率 (false-positive)实际为1-召回率：

• DLBCL的预测假阳性率指所有实际为FL的样本被错误的预测为DLBCL的比例；
• FL的预测假阳性率指所有实际为DLBCL的样本被错误的预测为FL的比例。

\[\begin{align} 假阳性率(DLBCL) &= \frac{8}{11+8} = 0.421 \\ 假阳性率(FL) &= \frac{2}{56+2} = 0.034 \end{align}\]

2.1.5 F1得分

Precision值和Recall值是既矛盾又统一的两个指标，为了提高Precision值，分类器需要尽量在“更有把握”时才把样本预测为正样本，但此时往往会因为过于保守而漏掉很多“没有把握”的正样本，导致Recall值降低。

F1分数（F1-score）是分类问题的一个衡量指标。一些多分类问题的机器学习竞赛，常常将F1-score作为最终测评的方法。它是某一个预测分类精准率和召回率的调和平均数，最大为1，最小为0。

\[\begin{align} F1 &= 2 * \frac{召回率*精准率}{召回率+精准率} \\ F1(DLBCL) &= 2 * \frac{0.875*0.966}{0.875+0.966} = 0.918 \\ F1(FL) &= 2 * \frac{0.846*0.579}{0.846+0.579} = 0.687 \\ F1_{average} &= (0.918+0.687)/2 = 0.8025 \end{align}\]

在F1得分中，精准率 (所有预测为阳性的样品有多少为真的阳性)和召回率 (所有阳性样品有多少预测为阳性)的权重是一样的。实际计算时也可以不同。如F2(召回率重要程度为精准率2倍)和F0.5 (召回率重要程度为精准率的一半)。

\[\begin{align} F1 &= 2 * \frac{召回率*精准率}{召回率+精准率} \\ F2 &= (1+2^2) * \frac{召回率*精准率}{召回率+(2^2*精准率)} \\ F_{\beta} &= (1+{\beta}^2) * \frac{召回率*精准率}{召回率+({\beta}^2*精准率)} \\ \end{align}\]

2.1.6 Kappa系数

Kappa系数，其也是评估分类准确性的一个指标。在模型评估指标一文有提到，准确性值在各个分类样本不平衡时会更多偏向样品多的类。而Kappa系数则可以综合评估这种不平衡性。Kappa系数在-1和1之间，值越大表示模型性能越好。

• Kappa=0说明模型和瞎猜差不多。
• Kappa>0.4说明模型还行。
• Kappa>0.4说明模型挺好的。
• 这几个标准未找到确切文献，仅供参考来理解 Kappa 系数。

其计算公式如下 (数据越不平衡，\(p_e\) 值就会越大，kappa 值就会越小 )：

$$\[\begin{align} kappa &= \frac{p_o-p_e}{1-p_e} \\ p_o &= \frac{混淆矩阵对角线元素之和}{混淆矩阵所有元素之和} \ \ \ \ \ \ (==等同于准确率)\\ p_e &= \frac{\sum_{i}第i 行元素之和*第 i列元素之和}{(\sum矩阵所有元素)^2} \\ p_o &= \frac{56+11}{56+8+2+11} = 0.8701299 \\ p_e &= \frac{(56+8)*(56+2) + (2+11)*(8+11)}{(56+8+2+11)^2} = 0.6677349 \\ kappa &= \frac{0.8701299-0.6677349}{1-0.6677349} = 0.6091371 \end{align}\] $$

2.1.7 ROC曲线 {ROC}

ROC (Receiver Operating Characteristic)特征曲线就是横轴为假阳性率，纵轴为真阳性率的一条曲线。这条曲线越陡越好，说明在较低的假阳性率时可以获得较高的真阳性率。

Figure 2.1: 根据阈值设定的变化，模型的假阳性率和真阳性率随之变化，形成了ROC曲线。来源于：https://zh.wikipedia.org/wiki/ROC%E6%9B%B2%E7%BA%BF

那么ROC曲线是怎么绘制的？假设有一个预测结果如下：

probability <- data.frame(Original_class= c("DLBCL", "DLBCL", "DLBCL", "DLBCL", 
                                            "DLBCL", "FL", "DLBCL","FL", "FL"),
                          Predicted_socre_for_sample_in_class_DLBCL=seq(0.9,0.1,-0.1))
probability

##   Original_class Predicted_socre_for_sample_in_class_DLBCL
## 1          DLBCL                                       0.9
## 2          DLBCL                                       0.8
## 3          DLBCL                                       0.7
## 4          DLBCL                                       0.6
## 5          DLBCL                                       0.5
## 6             FL                                       0.4
## 7          DLBCL                                       0.3
## 8             FL                                       0.2
## 9             FL                                       0.1

如果设置Predicted_socre_for_sample_in_class_DLBCL:

• >0.75为阈值标准，那么灵敏度=2/6=0.33，假阳性率为1-3/3=0;
• >0.65为阈值标准，那么灵敏度=3/6=0.50，假阳性率为1-3/3=0;
• >0.55为阈值标准，那么灵敏度=4/6=0.67，假阳性率为1-3/3=0;
• >0.45为阈值标准，那么灵敏度=5/6=0.83，假阳性率为1-3/3=0;
• >0.35为阈值标准，那么灵敏度=5/6=0.83，假阳性率为1-2/3=0.33;
• >0.25为阈值标准，那么灵敏度=6/6=1.00，假阳性率为1-2/3=0.33;
• >0.15为阈值标准，那么灵敏度=6/6=1.00，假阳性率为1-1/3=0.66;
• >0.05为阈值标准，那么灵敏度=6/6=1.00，假阳性率为1-0/3=1.00;

还是写个程序来算吧。

thresholdL = seq(1,0,-0.05)
right_class = "DLBCL"
score_column = "Predicted_socre_for_sample_in_class_DLBCL"
original_right = sum(probability$Original_class == right_class)
original_wrong = sum(probability$Original_class != right_class)

tpr_fpr <- function(probability, score_column, threshold, right_class, original_right, original_wrong){
  pass_threshold = as.vector(probability[probability[[score_column]]>threshold,1])
  # print(pass_threshold)
  pass_threshold_true = sum(pass_threshold == right_class)
  pass_threshold_false = sum(pass_threshold != right_class)
  tpr <- pass_threshold_true/original_right
  fpr <- pass_threshold_false/original_wrong
  return(c(threshold=threshold, tpr=tpr, fpr=fpr, right_class=right_class))
}

ROC_data = as.data.frame(do.call(rbind, lapply(thresholdL, tpr_fpr, 
                                               probability=probability, 
                                               score_column = score_column, 
                                               right_class=right_class, 
                                               original_right=original_right, 
                                               original_wrong=original_wrong)))
ROC_data$tpr <- as.numeric(ROC_data$tpr)
ROC_data$fpr <- as.numeric(ROC_data$fpr)

输出结果如下：

Table 2.1: ROC curve data

threshold	tpr	fpr	right_class
1	0.0000000	0.0000000	DLBCL
0.95	0.0000000	0.0000000	DLBCL
0.9	0.0000000	0.0000000	DLBCL
0.85	0.1666667	0.0000000	DLBCL
0.8	0.1666667	0.0000000	DLBCL
0.75	0.3333333	0.0000000	DLBCL
0.7	0.3333333	0.0000000	DLBCL
0.65	0.5000000	0.0000000	DLBCL
0.6	0.5000000	0.0000000	DLBCL
0.55	0.6666667	0.0000000	DLBCL
0.5	0.6666667	0.0000000	DLBCL
0.45	0.8333333	0.0000000	DLBCL
0.4	0.8333333	0.3333333	DLBCL
0.35	0.8333333	0.3333333	DLBCL
0.3	0.8333333	0.3333333	DLBCL
0.25	1.0000000	0.3333333	DLBCL
0.2	1.0000000	0.3333333	DLBCL
0.15	1.0000000	0.6666667	DLBCL
0.1	1.0000000	1.0000000	DLBCL
0.0499999999999999	1.0000000	1.0000000	DLBCL
0	1.0000000	1.0000000	DLBCL

简单绘制ROC曲线

library(ggplot2)

ggplot(ROC_data, aes(x=fpr, y=tpr, group=right_class)) + geom_step(direction="vh", color='red') + 
  geom_abline(intercept = 0, slope = 1)  + theme_classic() + 
  scale_y_continuous(expand=c(0,0)) + 
  xlab("False positive rate") + ylab("True positive rate") + coord_fixed(1)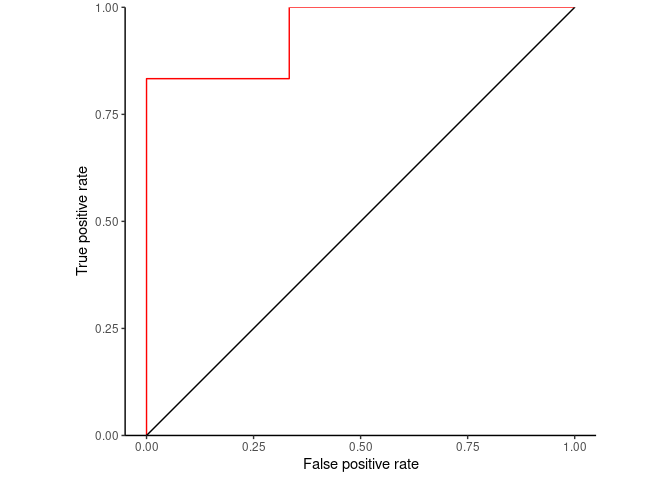

Figure 2.2: 简单绘制ROC曲线

如果right_class是FL呢？(这里只是用同一套数据，方便说明问题，实际需要对score取反)

thresholdL = seq(1,0,-0.05)
right_class = "FL"
score_column = "Predicted_socre_for_sample_in_class_DLBCL"
original_right = sum(probability$Original_class == right_class)
original_wrong = sum(probability$Original_class != right_class)

ROC_data2 = as.data.frame(do.call(rbind, lapply(thresholdL, tpr_fpr, 
                                               probability=probability, 
                                               score_column = score_column, 
                                               right_class=right_class, 
                                               original_right=original_right, 
                                               original_wrong=original_wrong)))
ROC_data2$tpr <- as.numeric(ROC_data2$tpr)
ROC_data2$fpr <- as.numeric(ROC_data2$fpr)


ggplot(ROC_data2, aes(x=fpr, y=tpr, group=right_class)) + geom_step(direction="vh", color='red') + 
  geom_abline(intercept = 0, slope = 1)  + theme_classic() + 
  scale_x_continuous(expand=c(0,0)) + xlab("False positive rate") + 
  ylab("True positive rate") + coord_fixed(1)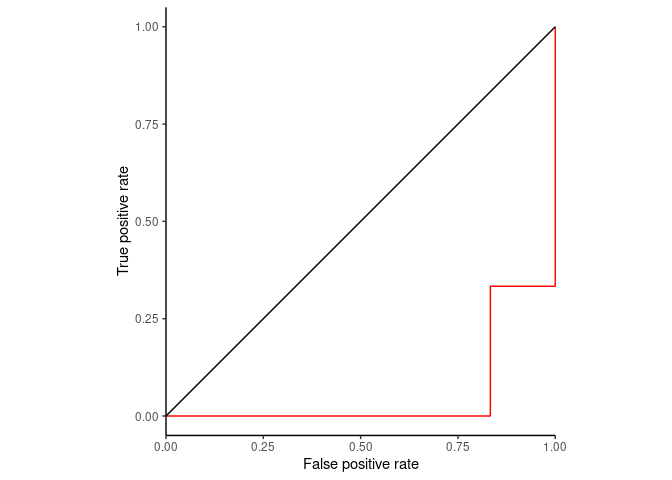

Figure 2.3: 简单绘制ROC曲线

从这张图可以看到，不管是根据FL计算，还是DLBCL计算，ROC曲线是一致的。

ROC_data3 = rbind(ROC_data, ROC_data2)

ggplot(ROC_data3, aes(x=fpr, y=tpr, color=right_class)) + geom_step(direction="vh") + 
  geom_segment(aes(x=0, xend=1, y=0, yend=1)) + theme_classic() + 
  xlab("False positive rate") + 
  ylab("True positive rate") + coord_fixed(1)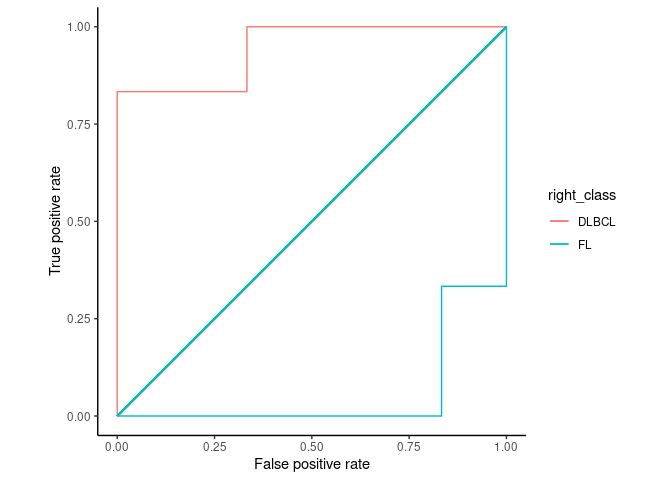

Figure 2.4: 选择不同分类作为阳性集，ROC曲线完全对称

同时ROC曲线不因样品不均衡而受影响。

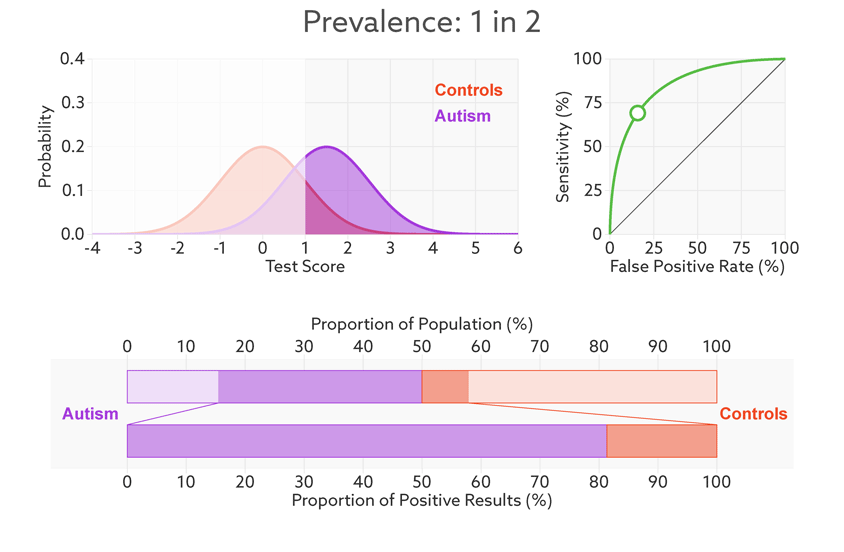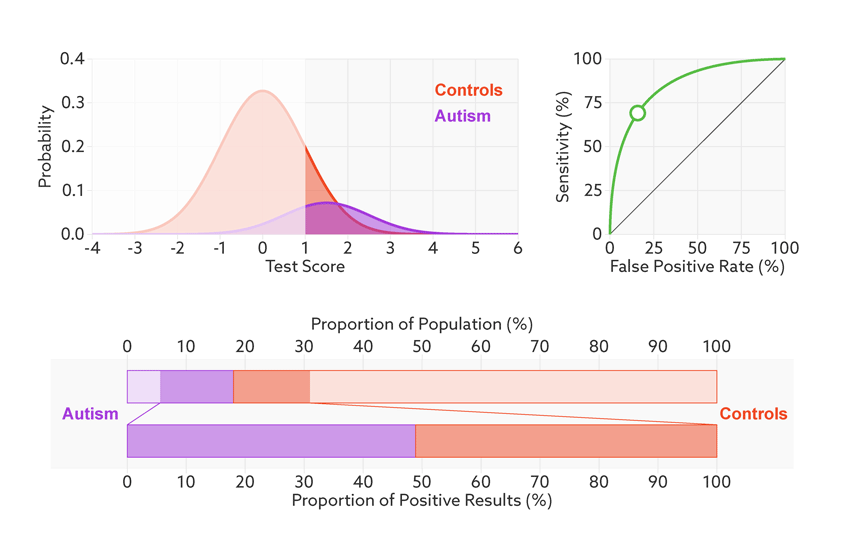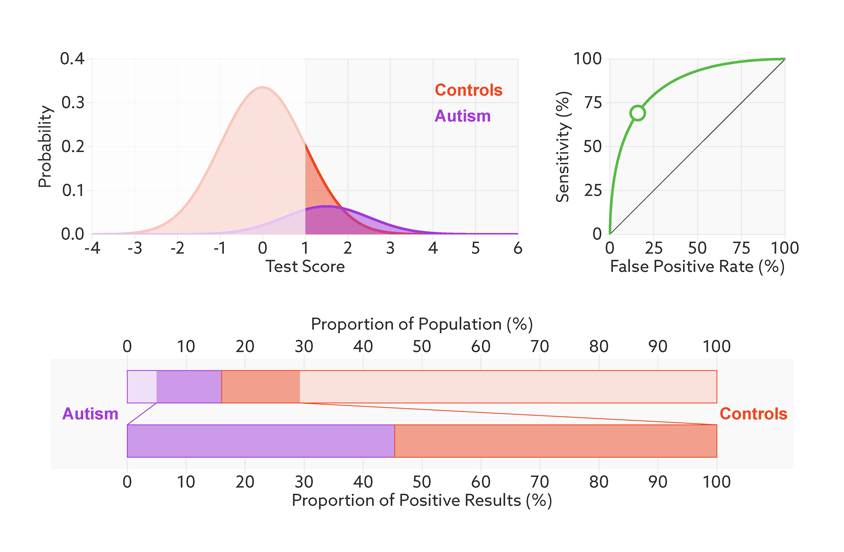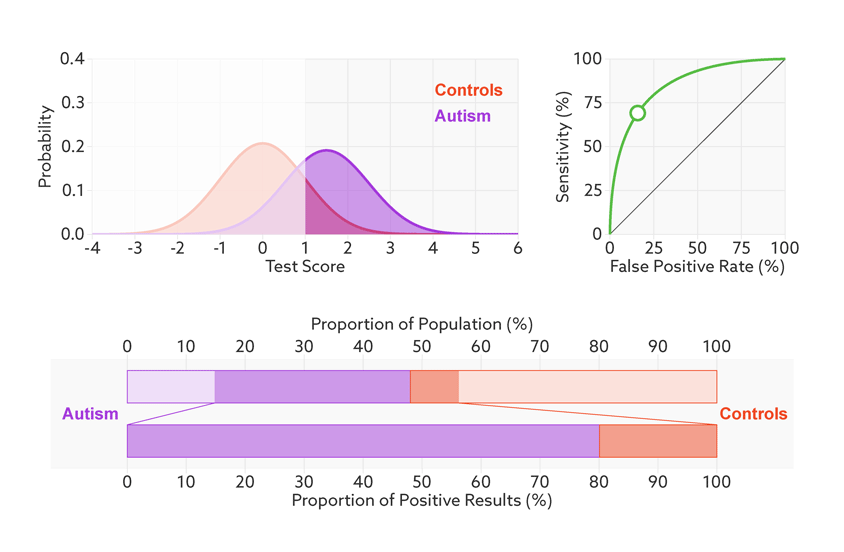
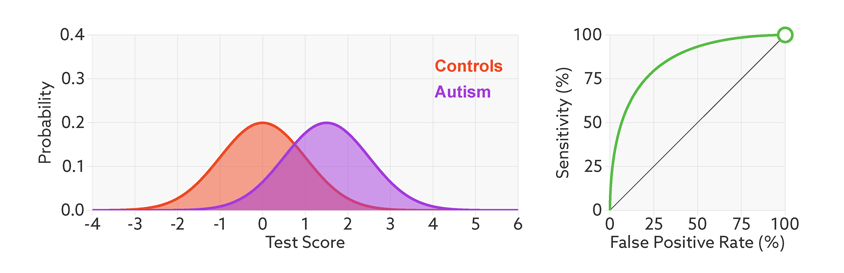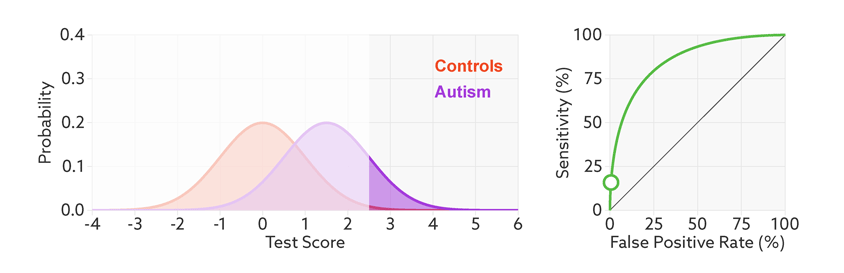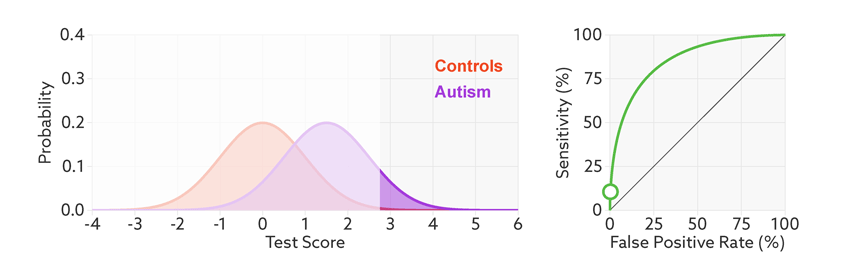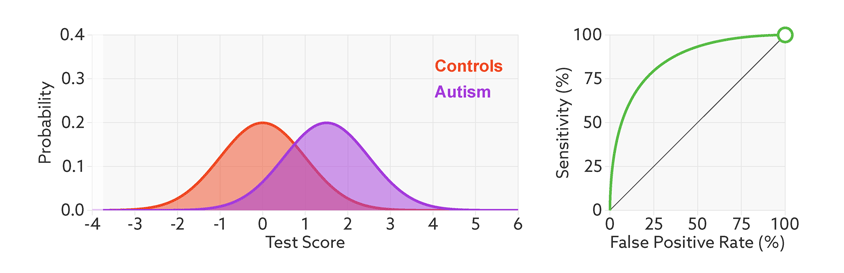
Figure 2.5: 当样品中自闭症病人的比例从1/2降到1/68时，精准率从81%降到6%。https://lukeoakdenrayner.wordpress.com/2018/01/07/the-philosophical-argument-for-using-roc-curves/

阈值的改变只是会改变真阳性率（灵敏度）和假阳性率。但是ROC曲线却不会变化。这只是我们控制假阳性率和灵敏度在合理范围时设置的过滤标准。

Figure 2.6: https://lukeoakdenrayner.wordpress.com/2018/01/07/the-philosophical-argument-for-using-roc-curves/

2.1.8 AUC (Area under curve)

如何根据ROC曲线判断一个模型的好坏呢？ROC曲线越陡越好，说明在较低的假阳性率时可以获得较高的真阳性率。一般通过曲线下面积AUC评估一个ROC曲线的好坏。一般模型的AUC值在0.5-1之间，值越大越好。

Figure 2.7: https://www.spectrumnews.org/opinion/viewpoint/quest-autism-biomarkers-faces-steep-statistical-challenges/

下面是一个经验展示。AUC=1是最理想的情况。AUC=0.5就是随机模型。如果总是AUC<0.5模型就可以反过来用。

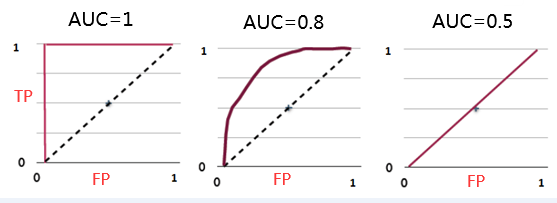
Figure 2.8: AUC经验展示

实际计算面积时并不是按几何图形进行计算的。通常根据AUC的物理意义进行计算。AUC值是一个概率值，当你随机挑选一个正样本以及负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值，AUC值越大，当前分类算法越有可能将正样本排在负样本前面，从而能够更好地分类。

假设有一套数据包含n个样本，M个正样本，N个负样本。每个样本计算一个Score值，所有样本按Score值排序。Score值最大的样本的rank为n（下面例子中是9），Score值次大的样品的rank为n-1（下面例子中是8）。正样品中rank最大的样本有rank_positive_max - 1 - (M-1)个负样本比他的score小 (M-1代表多少个正样本比)；正样品中rank第二大的样本有rank_positive_second - 1 - (M-2)个负样本比他的score小；

如下面样品a是rank最大的正样品其rank值为9，有3个负样品得分比其低。3怎么算的呢？

\(3 = 9 - 1 - (6-1) = rank1 - M\) (9是样品a的rank，-1是排除自身，6是正样本数，6-1 是除了a之外的正样本数)

如下面样品b是rank次大的正样品其rank值为8，有3个负样品得分比其低。3怎么算的呢？ \(3 = 8 - 1 - (6-2) = rank2 - M+1\) (8是样品b的rank，-1是排除自身，6是正样本数，6-2 是除了a,b之外的正样本数)

单独提取出后面的值就是M, M+1, M+2, M+3, ..., M + M-1，其加和就是

\[ \frac{M(1+M)}{2} \]

这样就可以总结出一个公式：

\[ AUC = \frac{(\sum_{positive}rank_i) - \frac{M(1+M)}{2}}{MxN} \]

probability_rank <- data.frame(Sample = letters[1:9],
                               Original_class= c("DLBCL", "DLBCL", "DLBCL", "DLBCL", "DLBCL", "FL", "DLBCL","FL", "FL"),
                          Predicted_socre_for_sample_in_class_DLBCL=seq(0.9,0.1,-0.1),
                          rank=seq(9,1,-1))
probability_rank

##   Sample Original_class Predicted_socre_for_sample_in_class_DLBCL rank
## 1      a          DLBCL                                       0.9    9
## 2      b          DLBCL                                       0.8    8
## 3      c          DLBCL                                       0.7    7
## 4      d          DLBCL                                       0.6    6
## 5      e          DLBCL                                       0.5    5
## 6      f             FL                                       0.4    4
## 7      g          DLBCL                                       0.3    3
## 8      h             FL                                       0.2    2
## 9      i             FL                                       0.1    1

写个函数计算

# 测试用例
# probability <- data.frame(Original_class= c("DLBCL", "DLBCL", "DLBCL", "DLBCL", "DLBCL", "FL", "DLBCL","FL", "FL"),
#                          Predicted_socre_for_sample_in_class_DLBCL=sample(seq(0,1,0.1),9))
# probability
AUC <- function(probability, score_column, class_column, right_class){
  sample_count = nrow(probability)
  positive_count = nrow(probability[probability[[class_column]]==right_class,])
  negative_count = sample_count - positive_count
  probability <- probability[rev(order(probability[[score_column]])),]
  probability$rank <- sample_count:1
  print(probability)
  rank_sum = sum(probability[probability[[class_column]]==right_class, "rank"])
  
  return((rank_sum - (positive_count+positive_count^2)/2)/(positive_count * negative_count))
}

AUC(probability, "Predicted_socre_for_sample_in_class_DLBCL", "Original_class", "DLBCL")

##   Original_class Predicted_socre_for_sample_in_class_DLBCL rank
## 1          DLBCL                                       0.9    9
## 2          DLBCL                                       0.8    8
## 3          DLBCL                                       0.7    7
## 4          DLBCL                                       0.6    6
## 5          DLBCL                                       0.5    5
## 6             FL                                       0.4    4
## 7          DLBCL                                       0.3    3
## 8             FL                                       0.2    2
## 9             FL                                       0.1    1

## [1] 0.9444444

2.1.9 PRC曲线和AUPRC

Precision值和Recall值是既矛盾又统一的两个指标，为了提高Precision值，分类器需要尽量在“更有把握”时才把样本预测为正样本，但此时往往会因为过于保守而漏掉很多“没有把握”的正样本，导致Recall值降低。

PRC (Precision recall curve)的纵轴是精准率，横轴是召回率。对于一个分类模型来说，其PRC线上的一个点代表着，在某一阈值下(随机森林模型默认阈值是0.5)，模型将大于该阈值的结果判定为正样本，小于该阈值的结果判定为负样本，此时返回结果对应的召回率和精确率。整条PRC曲线是通过将阈值从高到低移动而生成的。图1是P-R曲线样例图，其中实线代表 模型A的P-R曲线，虚线代表模型B的P-R曲线。原点附近代表当阈值最大时模型的精确率和召回率 (阈值越大，鉴定出的样品越真，能鉴定出的样品越少)。

knitr::include_graphics("images/PRC_example.jpg")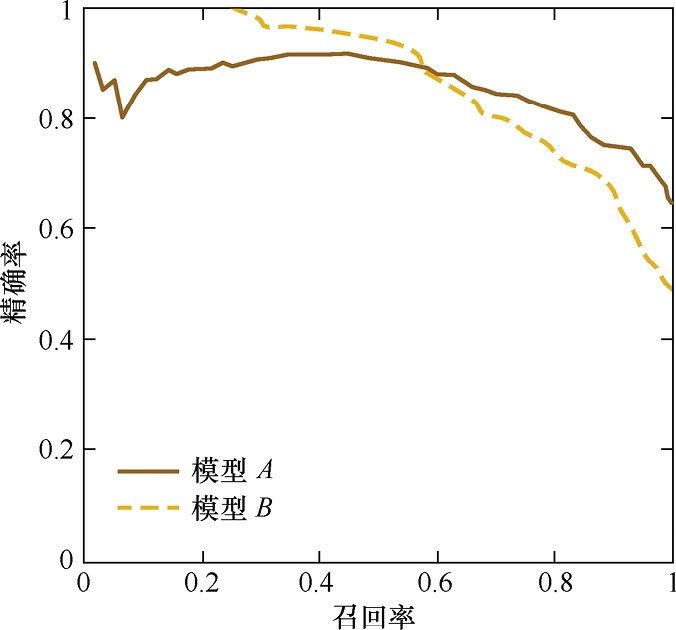

(#fig:PRC_example)Precision-recall curve.

从图可见，当召回率接近于0时，模型A的精准率为0.9，模型B的精准率是1，这说明模型B得分前几位的样本全部是真正的正样本，而模型A即使得分最高的几个样本也存在预测错误的情况。并且，随着召回率的增加，精准率整体呈下降趋 势。但是，当召回率为1时，模型A的精确率反而超过了模型B。这说明，只用某个点 (某个筛选阈值)对应的精准率和召回率是不能全面地衡量模型的性能，只有通过PRC的 整体表现，才能够对模型进行更为全面的评估。AUPRC就是类似于AUC的方式计算PRC曲线下方的面积，AUPRC越大，模型性能越好。

2.1.10 参考

• https://www.spectrumnews.org/opinion/viewpoint/quest-autism-biomarkers-faces-steep-statistical-challenges/
• https://www.cnblogs.com/gatherstars/p/6084696.html
• https://blog.csdn.net/qq_24753293/article/details/80942650
• https://zh.wikipedia.org/wiki/ROC%E6%9B%B2%E7%BA%BF
• OOB and confusion matrix https://stats.stackexchange.com/questions/30691/how-to-interpret-oob-and-confusion-matrix-for-random-forest
• https://towardsdatascience.com/confusion-matrix-for-your-multi-class-machine-learning-model-ff9aa3bf7826
• MSE for continuous data https://stats.stackexchange.com/questions/305046/best-way-to-evaluate-a-random-forest-model-accuracy-on-continuous-data
• https://stats.stackexchange.com/questions/190216/why-is-roc-auc-equivalent-to-the-probability-that-two-randomly-selected-samples?noredirect=1&lq=1
• An animation showing ROC curve https://stats.stackexchange.com/questions/105501/understanding-roc-curve
• PRC https://zhuanlan.zhihu.com/p/64963796

2.2 回归问题模型评估指标

2.2.1 RMSE (Root Mean Square Error) 均方根误差

衡量机器学习回归模型预测值与真实值之间的偏差，计算方式为

$$

RMSE =

: 表示模型的预测值

$$ ### MSE (Mean Square Error) 均方误差 {#mse}

衡量机器学习回归模型预测值与真实值之间的偏差，MSE是真实值与预测值的差值的平方然后求和平均。通过平方的形式便于求导，所以常被用作线性回归的损失函数。计算方式为

$$

MSE = _{i=1}^{n}( - y_i)^2 \

: 表示模型的预测值

$$ ### MAE (Mean Absolute Error) 平均绝对误差 {#mae}

绝对误差的平均值

$$

MAE = _{i=1}^{n} | - y_i| \

: 表示模型的预测值

$$

2.2.2 Reference

1. https://blog.csdn.net/FrankieHello/article/details/82024526

2.3 预测模型和分类模型 (Prediction and Classification)

区分预测模型和分类模型是很重要的一个事情。在很多决策应用中，分类模型代表着一个“不成熟”的决定，它组合了预测模型和决策制定，但剥夺了决策者对错误决定带来的损失的控制权 (如随机森林中的服从大多数原则，51棵树预测结果为患病``49棵树预测结果为正常与91棵树预测结果为患病``9棵树预测结果为正常返回的结果都是患病)。如果采样标准或损失/收益规 (在预测疾病时，更看重敏感性而非假阳性)则发生改变，分类模型也需要相应的改变。而预测模型是与决策分开的，可用于任何决策制定。

分类模型适用于频繁发生的非随机性(或者说确定性)的结果，而不适用于两个个体有同样的输入而输出却不同的情况。对于后者，模型的趋势（比如概率）则是关键因素。

分类模型的适用条件：

1. 分类结果很不同
2. 分类变量有很强的分类能力，可以在接近概率为1的情况下预测出其中一个分类结果

机器学习这一领域在某种程度上独立于统计学领域。因此，机器学习专家往往不强调概率思维。概率思维和理解不确定性和波动性 (variation)是统计学的重要特征。顺便说一下，关于概率思维最好的书之一是Nate Silver的The Signal and The Noise: Why So Many Predictions Fail But Some Don’t。在医学领域，David Spiegelhalter的《患者管理和临床试验中的概率预测》(Probability Prediction In Patient Management and Clinical Trials)是一篇经典论文。

摒除概率思维后，机器学习提倡频繁使用分类器，而不是使用风险预测模型。情况已经变得有些极端:许多机器学习专家实际上把逻辑回归 (logistic regression)列为一种分类方法(其实不是)。我们现在需要认真思考：分类真正意味着什么。分类实际上是一种决策。最佳决策需要充分利用现有数据来进行预测，并通过最小化损失函数/最大化效用函数来做出决策。不同的终端用户有不同的损失函数/效用函数 (在预测疾病时，如更看重敏感性，还是假阳性)，进而有不同的决策风险阈值。分类模型则假设每个用户都有相同的效用函数，就是分类系统所用的效用函数。

分类通常是一种被迫的选择。比如在市场营销中，广告预算是固定的，分析师通常还没有笨到直接使用模型把潜在客户归类为需要忽略的人或需要花费资源进行投放的人。相反，他们对概率进行建模，根据潜在客户购买产品的估计概率对其进行排序绘制一个Lift曲线。为了获得“最大的效果”，营销人员会选择n个可能性最高的客户作为目标进行广告投放。这是合理的，而且不需要分类。

模型使用者(如医生)经常提出的一个观点是，最终他们需要做出二元决策 (binary decision)，因此需要进行二元分类。而事实并非如此。首先，通常情况下，当预测出患病的概率是中等时，最好的决定是不做决定;去收集更多数据。在许多其他情况下，决定是可撤销的，例如，医生开始给病人低剂量的药物，然后决定是否改变剂量或更换药物。在外科治疗中，动手术的决定是不可改变的，但何时动手术取决于外科医生和病人，并取决于疾病的严重程度和症状。无论如何，如果需要进行二元分类，必须在所有情况都考虑到时，而非在数据建模时。

什么时候强制做出选择是合适的?我认为需要考虑这个问题是机械的 (确定性的)还是随机/概率的。机器学习的提倡者经常想把为前者 (机械性问题)所做的方法应用到存在生物变异、抽样变化和测量误差的问题上。而实际上最好是将分类模型仅仅应用于高信噪比的情况下，比如有一个已知的黄金标准，可以重复实验，每次得到几乎相同的结果。模式识别就是一个例子:

• 视觉、声音、化学成分等。如果创建一个光学字符识别算法 (OCR),该算法可以被任意数量的样品进行训练并尝试把图像分类为字母A, B,……等。 这样一个分类器的用户可能没有时间来考虑每个分类是否足够可信。但这种分类器信噪比是极高的。此外，每个字母都有一个“正确”答案。这种情况主要是机械性或非随机性的结果。而预测死亡或疾病时，两个症状相同的患者却很容易有不同的疾病发展方向。

当预测概率居中时，或者当结果有固有的随机性时，就需要进行概率估计。概率的一个优点是，它们是自己的错误的度量。如果预测疾病发生的概率是0.1，而当前的决定是不进行治疗；这个决定犯错的概率也是0.1。而如果发病概率是0.4，这会促使医生进行另一次实验检测或或采用活检等其它检测方式。当信噪比较小时，分类模型通常不是一个好的应用方式; 而是需要对趋势也就是概率进行建模。

美国气象局一直用概率来预测降雨。我不想得到一个分类结论“今天要下雨”。而是想着是否带伞应该由我来根据下雨的概率权衡后作出决定。

无论是从事信用风险评分、天气预报、气候预测、市场营销、病人疾病的诊断，还是评估病人的预后，我都不想使用分类的方法。而是希望获得带有可信区间或置信区间的风险估计得分。我的观点是，机器学习分类器最好用于机械的/确定性的高信噪比的数据或应用场景中，而概率模型应该用于大多数其他情况。

这与许多分析师忽略的一个微妙问题有关。复杂的机器学习算法可以通过进行高阶交互等处理问题的复杂性，但在信噪比较低时需要大量的数据。基于可加性假设的回归模型(当它们是正确的时，它们在绝大多数情况都是正确的)可以在没有大量数据集的情况下产生准确的概率模型。当被预测的结果变量有两个以上的水平时，一个回归模型可以获得各种感兴趣的量，如预测均值、分位数、超标概率 (exceedance probabilities)、瞬时危险率 (instantaneous hazard rates)等。

分类模型的一个特殊问题也反映了这样一个重要概念。使用机器学习分类模型的用户都知道，一个高度不平衡的样本训练集会获得一个奇怪的二元分类器。例如，如果训练集中有1000名患者和100万名非患者，那么最佳分类器可能将每个人都划分为非患者;这样获得的正确率是0.999。出于这个原因，对数据进行子集抽样的奇怪做法被用来平衡训练集中样本的频率，从而产生看起来合理的分类器 (回归模型的用户永远不会为了得到答案而排除好的数据)。然后，他们必须以某种不明确的方式构造分类器，以弥补训练集中样本组成的偏差。很简单，一个基于发病率为1/2的情况训练的模型将不能应用于发病率为1/1000的新数据的预测。分类器必须在新的样本上重新训练，检测到的模式可能会发生很大的变化。另一方面，Logistic回归巧妙地处理了这种情况，要么(1)将导致患病率如此之低的变量作为预测变量，要么(2)只需要重新校准另一个发病率高的数据集的截距。分类器对发病率的极端依赖可能足以使一些研究人员总是使用概率估计，如logistic回归进行代替。人们甚至可以说，当结果变量的变化很小时，根本不应该使用分类器，而应该只对概率建模。

选择一种方法的关键因素之一是它应该具有正确统计属性的敏感的准确性评分规则。机器分类的专家很少有了解这一极其重要问题的背景，选择一个不正确的准确性得分，如正确分类的比例，将导致一个虚假的模型。这里对此进行了详细讨论。

2.3.1 References

1. https://www.fharrell.com/post/classification/
2. Road Map for Choosing Between Statistical Modeling and Machine Learning https://www.fharrell.com/post/stat-ml/

2.4 训练集、验证集、测试集

随机森林与其他机器学习方法不同的是存在OOB，相当于自带多套训练集和测试集，自己内部就可以通过OOB值评估模型的准确度 (Bootstrap方式)。其他一些机器学习方法却没有这一优势。

通常在有了一套数据时，需要拆分为训练集、测试集。数据集一般按比例8:2, 7:3，6:4等分为训练集和测试集。如果数据集很大，测试集不需要完全按比例分配，够用就好。

测试集完全不用于训练模型，是模型从未见过的数据。训练集在训练模型时可能会出现过拟合问题（过拟合指模型可以很好的匹配训练数据但预测其它数据时效果不好），所以一般需要在训练集中再分出一部分作为验证集，用于评估模型的训练效果和调整模型的超参数 (hyperparameter)，如随机森林的ntree和mtry。

如下图，展示了一套数据集的一般分配方式：

• 训练集用于构建模型。
• 验证集用于评估模型的一般错误率，并且基于此调整超参数（hyperparameter，如随机森林中的mtry），获得当前最优模型。
• 验证集不是必须的。如果不需要调整超参数，则可以不用验证集。
• 验证集获得的评估结果不是模型的最终效果，而是基于当前数据的调优结果。
• 使用所有训练集（含从中分出的验证集）数据和选择的最优超参数完成最终模型构建。
• 测试集测试评估最终模型指标，如准确率、敏感性等。

通俗地讲，训练集等同于上课学习知识，验证集等同于课后测验检测学习效果并且查漏补缺。测试集是期末考试评估这个模型到底怎样。

可参考的分配规则：

• 对于小规模样本集（几万量级），常用的分配比例是 60% 训练集、20% 验证集、20% 测试集。
• 对于大规模样本集（百万级以上），只要验证集和测试集的数量足够即可，例如有 100 w 条数据，那么留 1 w 验证集，1 w 测试集即可。1000 w 的数据，同样留 1 w 验证集和 1 w 测试集。
• 超参数越少，或者超参数很容易调整，那么可以减少验证集的比例，更多的分配给训练集。

训练集中的数据我们希望能更多地应用于训练，但也需要验证集初步评估模型和校正模型。

2.4.1 简单交叉验证

简单交叉验证是从训练集中选择一部分（如70%）作为新训练集，剩余一部分（如30%）作为验证集。基于此选出最合适模型或最优模型参数。然后再用全部的训练集训练该选择的模型。其在一定程度上可以避免过拟合事件的发生。但基于70%训练集评估的最优模型是否等同于基于所有训练集的最优模型存疑。不同大小的验证集获得的评估结果差异较大，单纯按比例划分会导致无法选到最好的模型。另外如果训练集较小再如此分割后，训练集数目就更少了，不利于获得较好的训练模型。

2.4.2 K-fold交叉验证

所以就提出了交叉验证的操作，最常用的是K-fold交叉验证 (k-fold cross validation) 。

其目的是重复使用原始训练集中的数据，每一个样品都会被作为训练集参与训练模型，也会作为测试集参与评估模型。最大程度地利用了全部数据，当然也消耗了更多计算时间。

其操作过程如下：

1. 将训练集分成K份（如果训练集有m个样本，则每一份子集有m/K的样本；若不能整除其中一个或数个集合会样本少1个。）

2. 对于每一个模型（如随机森林中不同的mtry值，mtry=2, mtry=10时分别会构建出不同的模型；或不同的算法如随机森林、支持向量机、logistic 回归等）

   for j in 1, 2, 3, … K: 将训练集中除去第j份数据作为新训练集，用于训练模型 用第j份数据测试模型，获得该模型错误率

3. 经过第2步就得到了1个模型和K个错误；这K个错误率的均值和方差就是该模型的一般错误率。

4. 对每个模型重复2和3步骤，选择一般错误率最小的模型为当前最优模型。

5. 用所有的训练集数据训练当前的最优参数模型，获得最终训练结果。

6. 用独立的测试集评估模型错误率。

这一操作的优点是：

1. 所有训练集的样品都参与了每个模型的训练和评估，最大程度利用了数据。
2. 多个验证集多次评估，能更好的反应模型的预测性能。

下一步的关键就是如何选取K，通常为5或10 （10是最常用的经验值，但根据自己的数据集5，20也都可能获得比较好的结果）。

K越大，新训练集与总训练集大小差别越小，评估偏差也最小。 但计算量也会加大，运行时间需要更多。

极端情况下K=m，每个子数据集都只有 1 个样品，这也被称为LOOCV - leave one out-cross validation。

2.4.3 举个例子 - 2折交叉验证

假设有一个数据集，包含6个样品。

# 假设有一个数据集，包含 6 个样品
m = 6
train_set <- paste0('a', 1:m)
train_set

## [1] "a1" "a2" "a3" "a4" "a5" "a6"

利用其构建2-折交叉验证数据集。

K = 2
set.seed(1)
# 下面这行代码随机从1:K 中有放回的选取与样品数目一致的索引值
# 从属于相同索引值的样本同属于一个fold
kfold <- sample(1:K, size=m, replace=T)
kfold

## [1] 1 2 1 1 2 1

从下面数据可以看出，每个子集的大小不同。这通常不是我们期望的结果。

table(kfold)

## kfold
## 1 2 
## 4 2

修改如下，再次获取kfold:

kfold <- sample(rep(1:K, length.out=m), size=m, replace=F)
kfold

## [1] 1 2 2 2 1 1

这次每个fold的样品数目一致了。

# 如果 m/K 不能整除时，部分fold 样本数目会少
table(kfold)

## kfold
## 1 2 
## 3 3

然后构建每个fold的训练集和测试集

current_fold = 1
train_current_fold = train_set[kfold!=current_fold]
validate_current_fold = train_set[kfold==current_fold]

print(paste("Current sub train set:", paste(train_current_fold, collapse=",")))

## [1] "Current sub train set: a2,a3,a4"

print(paste("Current sub validate set:", paste(validate_current_fold, collapse=",")))

## [1] "Current sub validate set: a1,a5,a6"

写个函数循环构建。通过输出，体会下训练集和测试集的样品选择方式。

K_fold_dataset <- function(current_fold, train_set, kfold){
  train_current_fold = train_set[kfold!=current_fold]
  validate_current_fold = train_set[kfold==current_fold]
  c(fold=current_fold, sub_train_set=paste(train_current_fold, collapse=","), sub_validate_set=paste(validate_current_fold, collapse=","))
}

do.call(rbind, lapply(1:K, K_fold_dataset, train_set=train_set, kfold=kfold))

##      fold sub_train_set sub_validate_set
## [1,] "1"  "a2,a3,a4"    "a1,a5,a6"      
## [2,] "2"  "a1,a5,a6"    "a2,a3,a4"

Figure 2.9: https://www.youtube.com/watch?v=OoUX-nOEjG0

2.4.4 其它类型的交叉验证

• 如果K=m，则是留一法交叉验证 leave one out cross-validatiob, LOOCV。每个验证集都只有 1 个数据集，几乎所有样本在每次训练时都用到了，充分利用了数据。操作过程不涉及随机选择样品，因此是完全可重复的。但缺点是计算成本高。

• 分层交叉验证 (stratified): 根据数据集中的分组标签等比例的抽取数据，适用于非平衡数据集。

• 自助交叉验证: 类似rnadomForest自带的OOB方法

• 嵌套交叉验证：交叉验证的同时进行调参

2.4.5 可用数据集

测试数据集

• http://portals.broadinstitute.org/cgi-bin/cancer/datasets.cgi
• https://file.biolab.si/biolab/supp/bi-cancer/projections/info/DLBCL.html

2.4.6 Refercence

• 交叉验证概述 https://www.cnblogs.com/pinard/p/5992719.html
• 交叉验证 伪代码 https://www.cnblogs.com/jerrylead/archive/2011/03/27/1996799.html
• 交叉验证 伪代码 https://blog.csdn.net/lhx878619717/article/details/49079785
• cv 描述 https://machinelearningmastery.com/k-fold-cross-validation/
• manual cv 交叉验证 python API https://stackoverflow.com/questions/47960427/how-to-calculate-the-oob-of-random-forest
• 交叉验证 单验证集波动大 https://zhuanlan.zhihu.com/p/24825503
• 训练集 测试集 https://www.youtube.com/watch?v=OoUX-nOEjG0
• Kappa https://zhuanlan.zhihu.com/p/67844308
• 评估 K https://machinelearningmastery.com/how-to-configure-k-fold-cross-validation/
• Repeat K-fold https://machinelearningmastery.com/repeated-k-fold-cross-validation-with-python/
• 训练集、验证集、测试集 https://medium.com/@pkqiang49/%E4%B8%80%E6%96%87%E7%9C%8B%E6%87%82-ai-%E6%95%B0%E6%8D%AE%E9%9B%86-%E8%AE%AD%E7%BB%83%E9%9B%86-%E9%AA%8C%E8%AF%81%E9%9B%86-%E6%B5%8B%E8%AF%95%E9%9B%86-%E9%99%84-%E5%88%86%E5%89%B2%E6%96%B9%E6%B3%95-%E4%BA%A4%E5%8F%89%E9%AA%8C%E8%AF%81-9b3afd37fd58
• 分层交叉 https://zhuanlan.zhihu.com/p/48976706
• 训练集、验证集、测试集 https://stats.stackexchange.com/questions/19048/what-is-the-difference-between-test-set-and-validation-set