1 决策树
要理解随机森林,我们先学习下决策树。
1.1 决策树 - 把你做选择的过程呈现出来
决策树是一个很直观的跟我们日常做选择的思维方式很相近的一个算法。
如果有一个数据集如下:
data <- data.frame(x=c(0,0.5,1.1,1.8,1.9,2,2.5,3,3.6,3.7), color=c(rep('blue',5),rep('green',5)))
data## x color
## 1 0.0 blue
## 2 0.5 blue
## 3 1.1 blue
## 4 1.8 blue
## 5 1.9 blue
## 6 2.0 green
## 7 2.5 green
## 8 3.0 green
## 9 3.6 green
## 10 3.7 green那么假如加入一个新的点,其x值为1,那么该点对应的最可能的颜色是什么?
根据上面的数据找规律:
- 如果
x<2.0则对应的点颜色为blue - 如果
x>=2.0则对应的点颜色为green。
这就构成了一个只有一个决策节点的简单决策树。
决策树常用来回答这样的问题:给定一个带标签的数据集(标签这里对应我们的color列),怎么来对新加入的数据集进行分类?
如果数据集再复杂一些,如下:
data <- data.frame(x=c(0,0.5,1.1,1.8,1.9,2,2.5,3,3.6,3.7),
y=c(1,0.5,1.5,2.1,2.8,2,2.2,3,3.3,3.5),
color=c(rep('blue',3),rep('red',2),rep('green',5)))
data## x y color
## 1 0.0 1.0 blue
## 2 0.5 0.5 blue
## 3 1.1 1.5 blue
## 4 1.8 2.1 red
## 5 1.9 2.8 red
## 6 2.0 2.0 green
## 7 2.5 2.2 green
## 8 3.0 3.0 green
## 9 3.6 3.3 green
## 10 3.7 3.5 green- 如果
x>=2.0则对应的点颜色为green。 - 如果
x<2.0则对应的点颜色可能为blue,也可能为red。
这时就需要再加一个新的决策节点,利用变量y的信息。
Figure 1.2: Modified fron https://victorzhou.com/media/random-forest-post/decision-tree2.svg
这就是决策树,也是我们日常推理问题的一般方式。
1.2 训练决策树 - 确定决策树的根节点
第一个任务是确定决策树的根节点:选择哪个变量和对应阈值选择多少能给数据做出最好的区分。
比如上面的例子,我们可以先处理变量x,选择阈值为2 (为什么选2,是不是有比2更合适阈值,我们后续再说),则可获得如下分类:
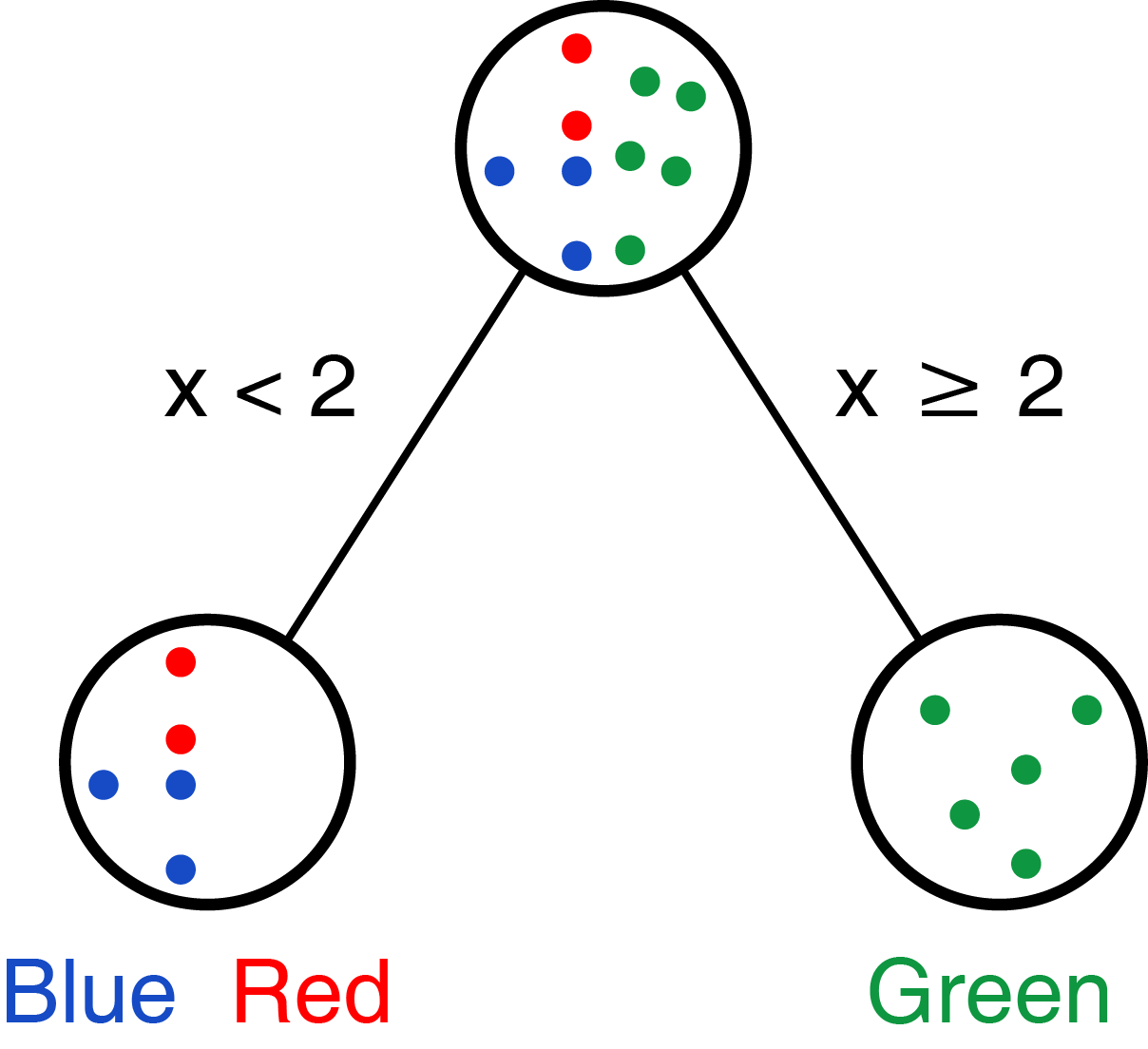
Figure 1.3: 变量 x 做根节点。
我们也可以先处理变量y,选择阈值为2,则可获得如下分类:
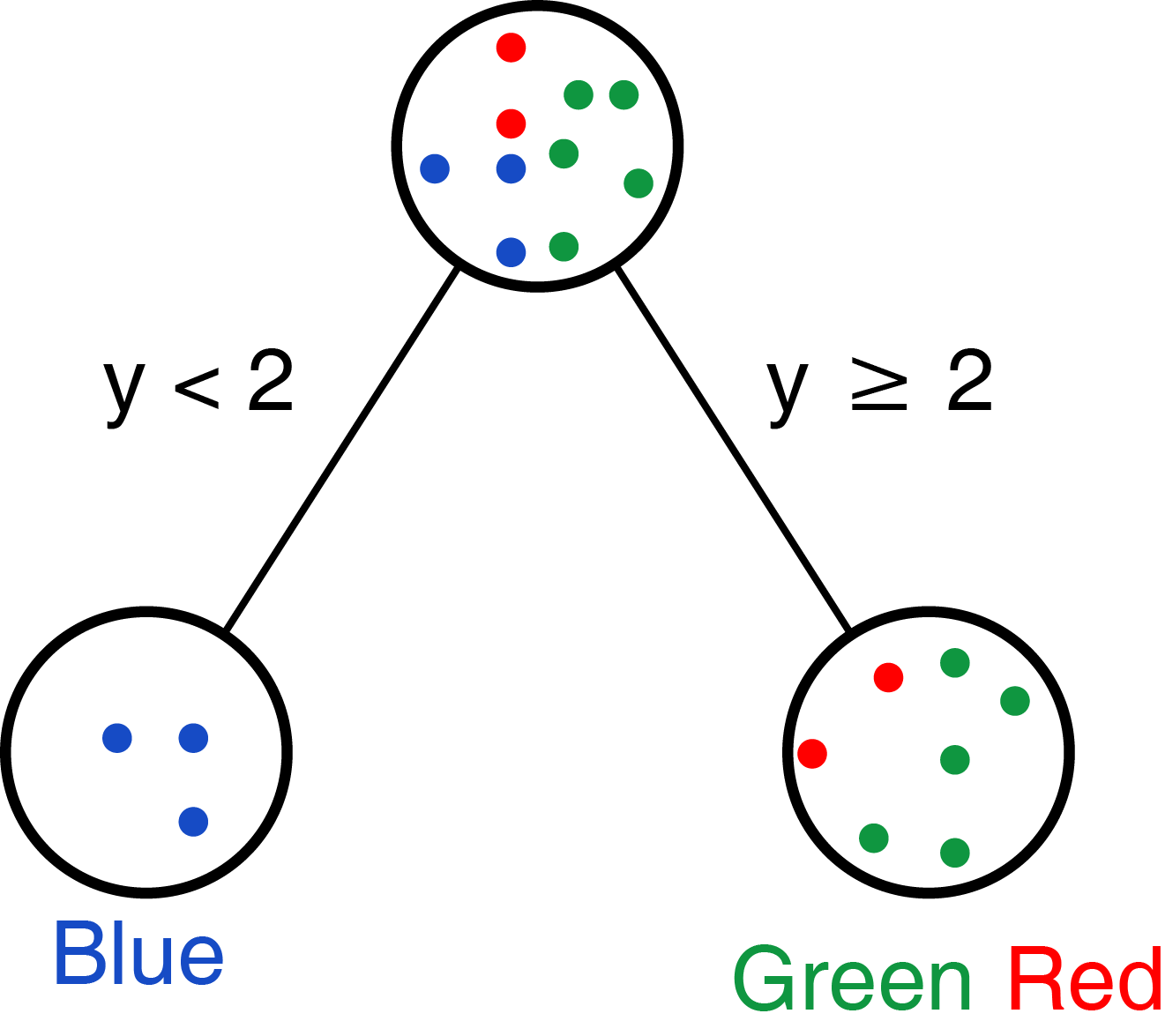
Figure 1.4: 变量 y 做根节点。
那实际需要选择哪个呢?实际我们是希望每个选择的变量和阈值能把不同的类分的越开越好;上面选择变量x分组时,Green完全分成一组;下面选择y分组时,Blue完全分成一组。
怎么评价呢?
这时就需要一个评价指标,常用的指标有Gini inpurity和Information gain。
1.2.1 Gini Impurity
在数据集中随机选择一个数据点,并随机分配给它一个数据集中存在的标签,分配错误的概率即为Gini impurity。
我们先看第一套数据集的初始状态,10个数据点,5个blue,5个green。从中随机选一个数据点,再随机选一个分类标签作为这个数据点的标签,分类错误的概率是多少?如下表,分类错误概率为0.25+0.25=0.5。
probility <- data.frame(Event=c("Pick Blue, Classify Blue",
"Pick Blue, Classify Green",
"Pick Green, Classify Blue",
"Pick Green, Classify Green"),
Probability=c(5/10 * 5/10, 5/10 * 5/10,
5/10 * 5/10, 5/10 * 5/10),
Type=c("Blue" == "Blue",
"Blue" == "Green",
"Green" == "Blue",
"Green" == "Green"))
probility## Event Probability Type
## 1 Pick Blue, Classify Blue 0.25 TRUE
## 2 Pick Blue, Classify Green 0.25 FALSE
## 3 Pick Green, Classify Blue 0.25 FALSE
## 4 Pick Green, Classify Green 0.25 TRUE我们再看第二套数据集,10个数据点,2个red,3个blue,5个green。从中随机选一个数据点,再随机选一个分类标签作为这个数据点的标签,分类错误的概率是多少?0.62。
probility <- data.frame(Event=c("Pick Blue, Classify Blue",
"Pick Blue, Classify Green",
"Pick Blue, Classify Red",
"Pick Green, Classify Blue",
"Pick Green, Classify Green",
"Pick Green, Classify Red",
"Pick Red, Classify Blue",
"Pick Red, Classify Green",
"Pick Red, Classify Red"
),
Probability=c(3/10 * 3/10, 3/10 * 5/10, 3/10 * 2/10,
5/10 * 3/10, 5/10 * 5/10, 5/10 * 2/10,
2/10 * 3/10, 2/10 * 5/10, 2/10 * 2/10),
Type=c("Blue" == "Blue",
"Blue" == "Green",
"Blue" == "Red",
"Green" == "Blue",
"Green" == "Green",
"Green" == "Red",
"Red" == "Blue",
"Red" == "Green",
"Red" == "Red"
))
probility## Event Probability Type
## 1 Pick Blue, Classify Blue 0.09 TRUE
## 2 Pick Blue, Classify Green 0.15 FALSE
## 3 Pick Blue, Classify Red 0.06 FALSE
## 4 Pick Green, Classify Blue 0.15 FALSE
## 5 Pick Green, Classify Green 0.25 TRUE
## 6 Pick Green, Classify Red 0.10 FALSE
## 7 Pick Red, Classify Blue 0.06 FALSE
## 8 Pick Red, Classify Green 0.10 FALSE
## 9 Pick Red, Classify Red 0.04 TRUEWrong_probability = sum(probility[!probility$Type,"Probability"])
Wrong_probability## [1] 0.62一个个算也不是办法,怎么总结出一个通用规律?
1.2.2 Gini Impurity计算公式
假如我们的数据点共有\(C\)个类,\(p(i)\)是从中随机拿到一个类为\(i\)的数据,Gini Impurity计算公式为:
\[ G = \sum_{i=1}^{C} p(i)*(1-p(i)) \]
对第一套数据集,10个数据点,5个blue,5个green。从中随机选一个数据点,再随机选一个分类标签作为这个数据点的标签,分类错误的概率是多少?错误概率为0.25+0.25=0.5。
\[\begin{align} 错误概率 G &= p(blue)*(1-p(blue)) + p(green)*(1-p(green)) \\ &= 5 / 10 * (1 - 5/10) + 5 / 10 * (1-5/10) \\ &= 0.5 \end{align}\]
对第二套数据集,10个数据点,2个red,3个blue,5个green。从中随机选一个数据点,再随机选一个分类标签作为这个数据点的标签,分类错误的概率是多少?0.62。
\[\begin{align} 错误概率 G &= p(blue)*(1-p(blue)) + p(green)*(1-p(green)) + p(red)*(1-p(red)) \\ &= 3 / 10 * (1 - 3/10) + 5 / 10 * (1 - 5/10) + 2 / 10 * (1 - 2/10) \\ &= 0.21 + 0.25 + 0.16 = 0.62 \end{align}\]
1.2.3 决策树分类后形成的两个分支的Gini Impurity
1.2.3.1 第一套数据集决策分支
对第一套数据集来讲,按照x<2分成两个分支,各个分支都只包含一个分类数据,各自的Gini Impurity值为0。
这是一个完美的决策树,把Gini Impurity为0.5的数据集分类为2个Gini Impurity为0的数据集。\(Gini Impurity==0\)是能获得的最好的分类结果。
\[\begin{align} G_{left} &= 5/5 * (1-5/5) = 0 \\ G_{right} &= 5/5 * (1-5/5) = 0 \end{align}\]
1.2.3.2 第二套数据集决策分支
第二套数据集,我们有两种确定根节点的方式,哪一个更优呢?
- 我们可以先处理变量
x,选择阈值为2,则可获得如下分类:

每个分支的Gini Impurity可以如下计算:
\[\begin{align} G_{left} &= 3/5 * (1-3/5) + 2/5 * (1-2/5) = 0.48 \\ G_{right} &= 5/5 * (1-5/5) = 0 \end{align}\]
当前决策的Gini impurity需要对各个分支包含的数据点的比例进行加权,即
\[\begin{align} G_{x-root} &= G_{left} * \frac{C_{blue}+C_{red}}{C_{toal}} + G_{right} * \frac{C_{green}}{C_{toal}}\\ &= 0.48 * (2+3)/10 + 0 \\ &= 0.24 \end{align}\]
- 我们也可以先处理变量
y,选择阈值为2,则可获得如下分类:

每个分支的Gini Impurity可以如下计算:
\[\begin{align} G_{left} &= 3/3 * (1-3/3) = 0 \\ G_{right} &= 2/7 * (1-2/7) + 5/7 * (1-5/7) = 0.41 \end{align}\]
当前决策的Gini impurity需要对各个分支包含的数据点的比例进行加权,即
\[\begin{align} G_{y- root} &= G_{left} * \frac{C_{blue}}{C_{toal}} + G_{right} * \frac{C_{green}+C_{red}}{C_{toal}} \\ &= 0 + 0.41 * (2+5)/10 \\ &= 0.29 \end{align}\]
两个数值比较0.24<0.29,选择x作为第一个分类节点是我们第二套数据第一步决策树的最佳选择。
前面手算单个变量、单个分组不算麻烦,也是个学习的过程。后续如果有更多变量和阈值时,再手算就不合适了。下面我们通过暴力方式自写函数训练决策树。
当前计算的结果,可以作为正对照,确定后续函数结果的准确性。
1.3 训练决策树 - 确定根节点的分类阈值
Gini impurity可以用来判断每一步最合适的决策分类方式,那么怎么确定最优的分类变量和分类阈值呢?
最粗暴的方式是,我们遍历每个变量的每个可能的阈值来进行决策分类,选择具有最低Gini impurity值的分类组合。这不是最快速的解决问题的方式,但是最容易理解的方式。
1.3.1 定义计算Gini impurity的函数
data <- data.frame(x=c(0,0.5,1.1,1.8,1.9,2,2.5,3,3.6,3.7),
y=c(1,0.5,1.5,2.1,2.8,2,2.2,3,3.3,3.5),
color=c(rep('blue',3),rep('red',2),rep('green',5)))
data## x y color
## 1 0.0 1.0 blue
## 2 0.5 0.5 blue
## 3 1.1 1.5 blue
## 4 1.8 2.1 red
## 5 1.9 2.8 red
## 6 2.0 2.0 green
## 7 2.5 2.2 green
## 8 3.0 3.0 green
## 9 3.6 3.3 green
## 10 3.7 3.5 green首先定义个函数计算每个分支的Gini_impurity。
Gini_impurity <- function(branch){
# print(branch)
len_branch <- length(branch)
# 防止被除数为0
if(len_branch==0){
return(0)
}
# 获取每个类的元素数目
table_branch <- table(branch)
# 每个类中的点被随机错误分配标签的概率
wrong_probability <- function(x, total) (x/total*(1-x/total))
# 加和总概率
return(round(sum(sapply(table_branch, wrong_probability, total=len_branch)),5))
}测试下,没问题。
Gini_impurity(c(rep('a',2),rep('b',3)))## [1] 0.48再定义一个函数,计算每次决策 获得的两个分支的总Gini impurity。
Gini_impurity_for_split_branch <- function(threshold, data, variable_column,
class_column, Init_gini_impurity=NULL){
total = nrow(data)
# 计算左分支和对应的Gini_impurity
left <- data[data[variable_column]<threshold,][[class_column]]
left_len = length(left)
left_table = table(left)
left_gini <- Gini_impurity(left)
# 计算右分支和对应的Gini_impurity
right <- data[data[variable_column]>=threshold,][[class_column]]
right_len = length(right)
right_table = table(right)
right_gini <- Gini_impurity(right)
# 加权Gini impurity
total_gini <- left_gini * left_len / total + right_gini * right_len /total
result = c(variable_column, threshold,
paste(names(left_table), left_table, collapse="; ", sep=" x "),
paste(names(right_table), right_table, collapse="; ", sep=" x "),
total_gini)
names(result) <- c("Variable", "Threshold", "Left_branch", "Right_branch", "Gini_impurity")
# 如果提供了初始未拆分时的Gini impurity,则计算Gini gain。
if(!is.null(Init_gini_impurity)){
Gini_gain <- Init_gini_impurity - total_gini
result = c(variable_column, threshold,
paste(names(left_table), left_table, collapse="; ", sep=" x "),
paste(names(right_table), right_table, collapse="; ", sep=" x "),
Gini_gain)
names(result) <- c("Variable", "Threshold", "Left_branch", "Right_branch", "Gini_gain")
}
return(result)
}测试下,跟之前计算的结果一致:
as.data.frame(rbind(Gini_impurity_for_split_branch(2, data, 'x', 'color'),
Gini_impurity_for_split_branch(2, data, 'y', 'color')))## Variable Threshold Left_branch Right_branch Gini_impurity
## 1 x 2 blue x 3; red x 2 green x 5 0.24
## 2 y 2 blue x 3 green x 5; red x 2 0.2857121.3.2 暴力决策根节点和阈值
基于前面定义的函数,遍历每一个可能的变量和阈值。
首先看下基于变量x的计算方法:
uniq_x <- sort(unique(data$x))
# 计算相邻 2 个值得均值
delimiter_x <- zoo::rollmean(uniq_x,2)
impurity_x <- as.data.frame(do.call(rbind, lapply(delimiter_x, Gini_impurity_for_split_branch,
data=data, variable_column='x', class_column='color')))
print(impurity_x)## Variable Threshold Left_branch Right_branch
## 1 x 0.25 blue x 1 blue x 2; green x 5; red x 2
## 2 x 0.8 blue x 2 blue x 1; green x 5; red x 2
## 3 x 1.45 blue x 3 green x 5; red x 2
## 4 x 1.85 blue x 3; red x 1 green x 5; red x 1
## 5 x 1.95 blue x 3; red x 2 green x 5
## 6 x 2.25 blue x 3; green x 1; red x 2 green x 4
## 7 x 2.75 blue x 3; green x 2; red x 2 green x 3
## 8 x 3.3 blue x 3; green x 3; red x 2 green x 2
## 9 x 3.65 blue x 3; green x 4; red x 2 green x 1
## Gini_impurity
## 1 0.533331
## 2 0.425
## 3 0.285712
## 4 0.316668
## 5 0.24
## 6 0.366666
## 7 0.457142
## 8 0.525
## 9 0.577782再包装2个函数,一个计算单个变量为决策节点的各种可能决策的Gini impurity (其实就是把上面那几行代码包起来), 另一个计算所有变量依次作为决策节点的各种可能决策的Gini impurity。
# 计算单个变量为决策节点的各种可能决策的`Gini impurity`
Gini_impurity_for_all_possible_branches_of_one_variable <- function(data, variable, class, Init_gini_impurity=NULL){
# 计算相邻2个值的均值作为分类阈值
uniq_value <- sort(unique(data[[variable]]))
delimiter_value <- zoo::rollmean(uniq_value,2)
# 依次调用函数Gini_impurity_for_split_branch,计算每次决策后总的Gini impurity
impurity <- as.data.frame(do.call(rbind, lapply(delimiter_value,
Gini_impurity_for_split_branch, data=data,
variable_column=variable,
class_column=class,
Init_gini_impurity=Init_gini_impurity)))
# 确定排序方式并排序
# 如果是Gini_impurity则从小到大排序,越小越好
# 如果是Gini_gain则从大到小排序,越大越好
if(is.null(Init_gini_impurity)){
decreasing = F
} else {
decreasing = T
}
impurity <- impurity[order(impurity[[colnames(impurity)[5]]], decreasing = decreasing),]
return(impurity)
}
# 计算所有变量依次作为决策节点的各种可能决策的`Gini impurity`
# 计算同一层级,根据各个变量的各个阈值所做的决策的Gini impurity
Gini_impurity_for_all_possible_branches_of_all_variables <- function(data, variables, class, Init_gini_impurity=NULL){
# 循环调用函数Gini_impurity_for_all_possible_branches_of_one_variable
one_split_gini <- do.call(rbind, lapply(variables,
Gini_impurity_for_all_possible_branches_of_one_variable,
data=data, class=class,
Init_gini_impurity=Init_gini_impurity))
# 再整体排序
if(is.null(Init_gini_impurity)){
decreasing = F
} else {
decreasing = T
}
one_split_gini[order(one_split_gini[[colnames(one_split_gini)[5]]], decreasing = decreasing),]
}测试下:
Gini_impurity_for_all_possible_branches_of_one_variable(data, 'x', 'color')## Variable Threshold Left_branch Right_branch
## 5 x 1.95 blue x 3; red x 2 green x 5
## 3 x 1.45 blue x 3 green x 5; red x 2
## 4 x 1.85 blue x 3; red x 1 green x 5; red x 1
## 6 x 2.25 blue x 3; green x 1; red x 2 green x 4
## 2 x 0.8 blue x 2 blue x 1; green x 5; red x 2
## 7 x 2.75 blue x 3; green x 2; red x 2 green x 3
## 8 x 3.3 blue x 3; green x 3; red x 2 green x 2
## 1 x 0.25 blue x 1 blue x 2; green x 5; red x 2
## 9 x 3.65 blue x 3; green x 4; red x 2 green x 1
## Gini_impurity
## 5 0.24
## 3 0.285712
## 4 0.316668
## 6 0.366666
## 2 0.425
## 7 0.457142
## 8 0.525
## 1 0.533331
## 9 0.577782两个变量的各个阈值分别进行决策,并计算Gini impurity,输出按Gini impurity由小到大排序后的结果。根据变量x和阈值1.95 (与上面选择的阈值2获得的决策结果一致)的决策可以获得本步决策的最好结果。
variables <- c('x', 'y')
Gini_impurity_for_all_possible_branches_of_all_variables(data, variables, class="color")## Variable Threshold Left_branch Right_branch
## 5 x 1.95 blue x 3; red x 2 green x 5
## 3 x 1.45 blue x 3 green x 5; red x 2
## 31 y 1.75 blue x 3 green x 5; red x 2
## 4 x 1.85 blue x 3; red x 1 green x 5; red x 1
## 6 x 2.25 blue x 3; green x 1; red x 2 green x 4
## 41 y 2.05 blue x 3; green x 1 green x 4; red x 2
## 2 x 0.8 blue x 2 blue x 1; green x 5; red x 2
## 21 y 1.25 blue x 2 blue x 1; green x 5; red x 2
## 51 y 2.15 blue x 3; green x 1; red x 1 green x 4; red x 1
## 7 x 2.75 blue x 3; green x 2; red x 2 green x 3
## 71 y 2.9 blue x 3; green x 2; red x 2 green x 3
## 61 y 2.5 blue x 3; green x 2; red x 1 green x 3; red x 1
## 8 x 3.3 blue x 3; green x 3; red x 2 green x 2
## 81 y 3.15 blue x 3; green x 3; red x 2 green x 2
## 1 x 0.25 blue x 1 blue x 2; green x 5; red x 2
## 11 y 0.75 blue x 1 blue x 2; green x 5; red x 2
## 9 x 3.65 blue x 3; green x 4; red x 2 green x 1
## 91 y 3.4 blue x 3; green x 4; red x 2 green x 1
## Gini_impurity
## 5 0.24
## 3 0.285712
## 31 0.285712
## 4 0.316668
## 6 0.366666
## 41 0.416664
## 2 0.425
## 21 0.425
## 51 0.44
## 7 0.457142
## 71 0.457142
## 61 0.516666
## 8 0.525
## 81 0.525
## 1 0.533331
## 11 0.533331
## 9 0.577782
## 91 0.577782
1.3.3 再决策第二个节点、第三个节点
第一个决策节点找好了,后续再找其它决策节点。如果分配到某个分支的点从属于多个class,则递归决策。
递归决策终止的条件是:
- 再继续向下分支不会降低
Gini impurity - 该分支的数据点属于同一分类组 (
Gini impurity = 0)
brute_descition_tree_result <- list()
brute_descition_tree_result_index <- 0
# 递归分支决策
brute_descition_tree <- function(data, measure_variable, class_variable, type="Root"){
# 计算初始Gini值
Init_gini_impurity <- Gini_impurity(data[[class_variable]])
# 确定当前需要决策的节点的最优变量和最优阈值
brute_force_result <- Gini_impurity_for_all_possible_branches_of_all_variables(
data, variables, class=class_variable, Init_gini_impurity=Init_gini_impurity)
# 输出中间计算结果
print(brute_force_result)
# 根据最优决策变量、阈值和Gini增益
split_variable <- brute_force_result[1,1]
split_threshold <- as.numeric(brute_force_result[1,2])
gini_gain = as.numeric(brute_force_result[1,5])
# print(gini_gain)
# 判断此次决策是否需要保留
if(gini_gain>0){
brute_descition_tree_result_index <<- brute_descition_tree_result_index + 1
brute_descition_tree_result[[brute_descition_tree_result_index]] <<-
c(type=type, split_variable=split_variable,
split_threshold=split_threshold)
# print(brute_descition_tree_result_index)
# print(brute_descition_tree_result)
# 决策左右分支
left <- data[data[split_variable]<split_threshold,]
right <- data[data[split_variable]>=split_threshold,]
# 分别对左右分支进一步决策
if(length(unique(left[[class_variable]]))>1){
brute_descition_tree(data=left, measure_variable, class_variable,
type=paste(brute_descition_tree_result_index, "left"))
}
if(length(unique(right[[class_variable]]))>1){
brute_descition_tree(data=right, measure_variable, class_variable,
type=paste(brute_descition_tree_result_index, "right"))
}
}
# return(brute_descition_tree_result)
}
brute_descition_tree(data, variables, "color")## Variable Threshold Left_branch Right_branch
## 5 x 1.95 blue x 3; red x 2 green x 5
## 3 x 1.45 blue x 3 green x 5; red x 2
## 31 y 1.75 blue x 3 green x 5; red x 2
## 4 x 1.85 blue x 3; red x 1 green x 5; red x 1
## 6 x 2.25 blue x 3; green x 1; red x 2 green x 4
## 41 y 2.05 blue x 3; green x 1 green x 4; red x 2
## 2 x 0.8 blue x 2 blue x 1; green x 5; red x 2
## 21 y 1.25 blue x 2 blue x 1; green x 5; red x 2
## 51 y 2.15 blue x 3; green x 1; red x 1 green x 4; red x 1
## 7 x 2.75 blue x 3; green x 2; red x 2 green x 3
## 71 y 2.9 blue x 3; green x 2; red x 2 green x 3
## 61 y 2.5 blue x 3; green x 2; red x 1 green x 3; red x 1
## 8 x 3.3 blue x 3; green x 3; red x 2 green x 2
## 81 y 3.15 blue x 3; green x 3; red x 2 green x 2
## 1 x 0.25 blue x 1 blue x 2; green x 5; red x 2
## 11 y 0.75 blue x 1 blue x 2; green x 5; red x 2
## 9 x 3.65 blue x 3; green x 4; red x 2 green x 1
## 91 y 3.4 blue x 3; green x 4; red x 2 green x 1
## Gini_gain
## 5 0.38
## 3 0.334288
## 31 0.334288
## 4 0.303332
## 6 0.253334
## 41 0.203336
## 2 0.195
## 21 0.195
## 51 0.18
## 7 0.162858
## 71 0.162858
## 61 0.103334
## 8 0.095
## 81 0.095
## 1 0.0866690000000001
## 11 0.0866690000000001
## 9 0.042218
## 91 0.042218
## Variable Threshold Left_branch Right_branch Gini_gain
## 3 x 1.45 blue x 3 red x 2 0.48
## 31 y 1.8 blue x 3 red x 2 0.48
## 2 x 0.8 blue x 2 blue x 1; red x 2 0.213336
## 21 y 1.25 blue x 2 blue x 1; red x 2 0.213336
## 4 x 1.85 blue x 3; red x 1 red x 1 0.18
## 41 y 2.45 blue x 3; red x 1 red x 1 0.18
## 1 x 0.25 blue x 1 blue x 2; red x 2 0.08
## 11 y 0.75 blue x 1 blue x 2; red x 2 0.08as.data.frame(do.call(rbind, brute_descition_tree_result))## type split_variable split_threshold
## 1 Root x 1.95
## 2 2 left x 1.45运行后,获得两个决策节点,绘制决策树如下:
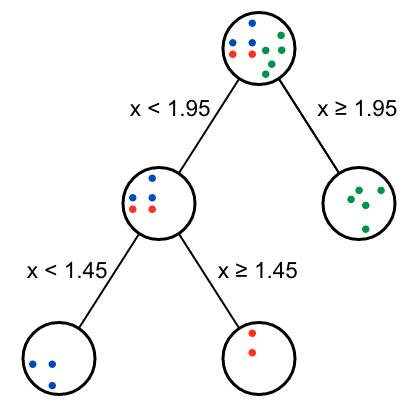
从返回的Gini gain表格可以看出,第二个节点有两种效果一样的分支方式。
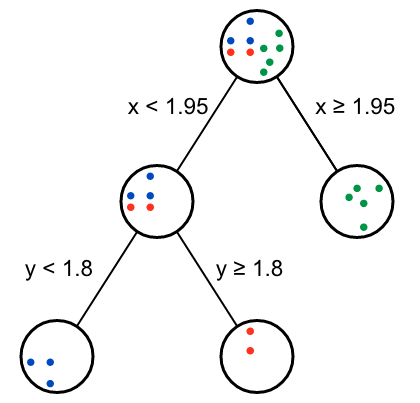
这样我们就用暴力方式完成了决策树的构建。