3 随机森林
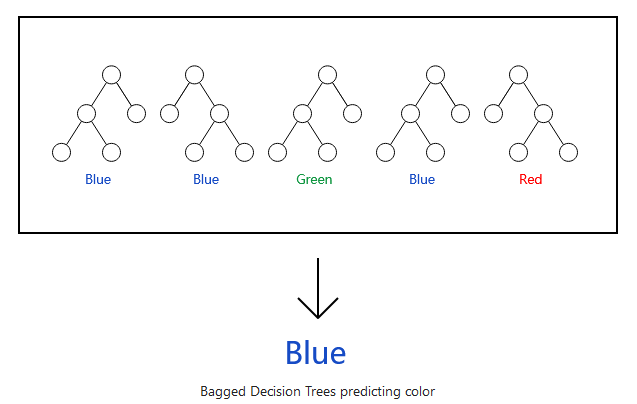
随机森林是基于集体智慧的一个机器学习算法,也是目前最好的机器学习算法之一。随机森林实际是一堆决策树的组合(正如其名,树多了就是森林了)。在用于分类一个新变量时,相关的检测数据提交给构建好的每个分类树。每个树给出一个分类结果,最终选择被最多的分类树支持的分类结果。(回归则是不同树预测出的值的均值)。
其优点是:
- 准确率最好的算法之一
- 对大数据集也能有效运算 (得益于第2次随机)
- 可以处理高维数据,且无需降维 (得益于第2次随机)
- 能够评估各个变量在分类问题中的重要性 (数据置换评估)
- 自带训练集和测试集,在构建模型时即可评估分类错误 (得益于第1次随机)
- 即便在大量缺失值情况下,也可准确进行缺失值插补
- 产生的树可以保存用于后续预测等使用
- 随机森林不会过拟合,只要内存足够,可以设置更多的树。一个
50,000 cases X 100 variables的数据集,普通电脑可以在3分钟构建100棵树 - 可以平衡不同分组样品多少引入的预测错误率
- 可以鉴定异常样品、可视化样品的相似性关系
3.1 随机森林的算法概述
决策树我们应该都暴力的理解了,下面我们看随机森林。
随机森林实际是一堆决策树的组合(正如其名,树多了就是森林了)。
这是一个简化版的理解,实际上要复杂一些。具体怎么做的呢?
假设有一个数据集包含n个样品, p个变量,也就是一个n X p的矩阵,采用下面的算法获得一系列的决策树:
- 从数据集中有放回地取出
n个样品作为训练集,训练1棵决策树。假如数据集有6个样品[a,b,c,d,e,f],第一次有放回地取出6个样品可能是[a,a,c,d,d,e],第二次有放回地取出6个样品可能是[a,c,c,d,e,e]。每棵树的训练集是不完全相同的,但样品数目是一样的,因为每个训练集内部包含重复样本。这一步称为Bagging (Bootstrap aggregating) 自助聚合。 - 每棵决策树构建时,通常随机抽取
m (m<<p)个变量进行每个节点决策变量的选择,m在选择每一层节点时不变。其意义是每次进行决策时只在随机选择的m个变量而不是全部变量中选择最好的分类变量,也是为了增强随机性。 - 每棵决策树野蛮生长,不剪枝。
- 重复第
1,2,3步t次,获得t棵决策树。
通过聚合t棵决策树做出最终决策:
- 分类问题:选择
t棵决策树中支持最多的类作为最终分类 (服从多数,majority vote) - 回归问题:计算
t棵决策树预测的数值的均值作为最终预测值
3.1.1 为什么要这么做呢?
在数据科学中,很大数目的相对不相关的模型的群体决策优于任何单个模型的决策。
随机森林的错误率取决于两个因素:
- 不同树之间的相关性越高,则错误率越大。这要求
m尽可能小。 - 每个决策树的分类强度越大,则错误率越小。这要求
m尽可能大。
m通常为\(\sqrt{num\_variable}\) (用于分类问题)或\(\frac{num\_variable}{3}\) (用于回归问题)。也可以通过oob (out-of-bag) error rate (自助聚合错误率)进行迭代调参选择分类效果最好的m。
3.1.2 随机森林工作机制
通过有放回采样的方式构建训练集时,通常有1/3的样品没有被选中,也就是不用于构建决策树。这些样品可以用来估计该训练集获得的决策树的分类错误率 (OOB), 也可以用来评估变量的重要性。
3.1.3 oob (out-of-bag) error rate (聚合错误率)
应用随机森林时,无需交叉验证或额外的测试集来评估错误率,而是在构建随机森林时,可自行评估:
- 每一个决策树构建时使用到的样本是不同的。因为是有放回地随机采样,在构建每棵树时,大约
1/3的样品不会被用到(验证集)。 - 这些没有被抽样到用于构建决策树的样品会用来测试该决策树的分类能力。理论上每个样品在
1/3的决策树中可作为验证样品获得一个分类结果和分类错误率。 - 聚合每个没有被抽样到的样品在所有其不被用于训练集构建的决策树的分类结果作为该样品的最终分类结果 (
Majority vote,可以理解为是一个小的随机森林对该样品的分类结果),与数据的原始分类一致则是分类正确,否则是分类错误。 - 所有分类错误的样品除以总样品即为构建的随机森林模型的错误率。(
i表示第i棵树)
$$\[\begin{align} OOB_{case_i} &= \begin{cases} 1 \text{ if predicted class for case i is wrong} \\ 0 \text{ if predicted class for case i is right} \\ 0 \text{ case i always in train sample} \end{cases} \\ OOB_{tree} &= \frac{\sum_{i=1}^{n}OOB_{case_i}}{n} \end{align}\]$$
3.1.4 变量重要性
对于每一棵随机决策树,统计其分类OOB数据集中所有样品正确分类的次数 (O)。随机排列OOB数据集中变量m的值 (打乱变量m在所有样品的原始值),再用该决策树分类,统计所有样品被正确分类的次数 (P)。这两个次数的差值(O-P)即为变量m在单棵决策树的分类重要性得分 (CS, classification score),其在所有分类树中的均值即为该变量的整体重要性得分 (ACS, avraged classification score)。
\[\begin{align} CS_{m}^{tree\_i} &= Count_{rightly\_classified} - Count_{rightly\_classified\_for\_random\_permutation} \\ ACS_{m} &= \frac{\sum_{i=1}^{t}CS_{m}^{tree\_i}}{t} \\ ACS_{m}^{zscore} &= \frac{ACS_{m}}{sd(CS_{m}^{tree\_1}, CS_{m}^{tree\_2},...,CS_{m}^{tree\_t})} \end{align}\]
通过大量数据测试发现,同一个变量不同决策树获得的CS的相关性很低,可以认为是彼此独立的。随后按照常规方式计算所有CS的标准差,ACS/sd(CS)获得Z-score值。假设Z-score服从正态分布,即可根据Z-score估计该变量的重要性程度。(后面的特征变量选择还有其他方式可进行筛选)
如果变量数目很多,也可只在第一次用所有变量评估,后续只评估第一次选出的最重要的一部分变量。
但是如果两个变量相关性比较强,随机置换一个变量时其对分类的影响效果有限,会高估变量的重要性。
3.1.5 Gini importance
Gini impurity得分是确定决策树每一层级节点和阈值的一个评判标准 (具体见1.2.1。每个变量 (m)贡献的Gini impurity的降低程度(GD(m))可以作为该变量重要性的一个评价标准。变量(m)在所有树中的GD(m)之和获得的变量重要性评估与上面通过随机置换数据获得的变量评估结果通常是一致的。
但一般不使用这个指标,因为实际应用时存在偏好性。
3.1.6 变量互作 Interactions
变量互作定义为,一个决策树通过变量m做了决策后的子节点可以更容易或更不容易通过变量k做决策。如果变量m与变量k相关,按m决策后,再按k决策就不容易分割因为已经被m分割了。
这也是基于两个变量m和k是独立的这一假设。通常通过每个变量作为决策节点时计算出的Gini impurity得分 (g(m)或 g(k),得分越低说明决策分割效果越少)作为评价依据。他们的差值g(m) - g(k)即为变量m和k的互作值,这个值越大,说明基于变量m分割后更有利于基于变量k分割。
3.1.7 相似性 Proximities
每棵决策树构建好后,用所有的数据作为输入获得每个样品在每个决策树的分类结果,然后计算每一对样品 (c1, c2)之间的相似度 (\(Proximity_i\))。如果两个样品分类到相同的分类节点,它们彼此的相似性加一。最终的相似度除以决策树的总数 (t)目获得任意一对样品标准化后的相似度值。这些值构成一个n X n (n为总样品数)的矩阵。这些值可后续用于缺失值填充、异常样品鉴定和对数据进行低维可视化。(i表示第i棵树)
$$\[\begin{align} Proximity_{i}(c1,c2) &= \begin{cases} 1 \text{ if class(c1)==class(c2)} \\ 0 \text{ if class(c1)!=class(c2)} \end{cases} \\ Proximity(c1,c2) &= \frac{\sum_{i=1}^{t} Proximity_{i}(c1,c2)}{t} \end{align}\]$$
- 初始化两个样品的相似性为
0 - 每个样品通过每一棵树预测其分类
- 如果样品
i和j预测分类到同一个节点,其相似性值加1 - 每对样品的相似性值累加并除以决策树的数目即为最终相似性值
- 最终获得一个对角阵
如果数据集较大,n X n的矩阵可能需要消耗比较多存储内存。这是可以使用n X t的矩阵来存储 (t是随机森林中决策树的数目)。用户也可以指定每个样品只保留最相似的nrnn个样本,以加快运算速度。
如果有测试数据集,测试集中的样品也可以与训练集中的样品计算两两相似度。
3.1.8 降维展示 Scaling
样品i和j的相似度定义为prox(i,j),这是一个不大于1的正数 (具体见前面公式{3.1.7})。1-prox(i,kj)则是样品i和j的欧式距离。这样就构成一个最大为n X n的距离矩阵。
随后就可以通过MDS方式计算其内积,求解特征值和特征向量。可类比于PCA分析,获得几个新的展示维度。通常绘制第1,2维就可以比较好的展示样品的分布。
3.1.9 原型 Prototypes
Prototypes是一种展示变量与分类关系的方式。对第j类,选择基于相似性获得的K近邻样品中落在j类最多的样品。这k个样品中,计算每个变量的中位数、第一四分位数和第三四分位数。这个中位数就是class j的原型 (prototype), 第一四分位数和第三四分位数则是原型的置信范围。对于第二个原型,按之前的步骤计算,只是不考虑上一步用到的k的样品。输出原型时,如果是连续变量,则用原型值减去第5分位数并除以第95分位数和第5分位数的差值。如果是区域变量,原型就是出现次数最多的值。
原型可用于聚类。
3.1.10 填充训练集中的缺失值
随机森林有两种方式填充缺失值。
第一种方式速度快。假设某个样品属于
class j,其变量m值缺失,如果变量m的值是数值型,则用class j中所有样品的变量m的值的中位数作为填充值;如果变量m的值是分类型,则用class j中所有样品出现次数最多的变量m的值作为填充值;第二种方式需要更多计算量但可以给出更好的结果,即便是存在大量缺失数据时。它只通过训练集填充缺失值。首先对缺失值做一个粗略的、非精确的填充。然后计算随机森林和样本相似性。
定义样品i的变量m的值为v(m,i),如果变量m为连续性数值变量,则其填充值为其它样品中变量m的值与该样品与样品i的相似性的乘积的均值 (n1是变量m不为缺失值的样品)。如果变量m为分类型变量, 则替换其为所有样品最频繁出现的值(计算频率时需要用根据每个样品与样品i的相似性进行加权)。
\[v(m,i) = \frac{\sum_{x=1}^{n1}{prox(i,x)* v(m,x)}}{n1}\]
随后使用填充后的数据集迭代构建随机森林模型,计算新的填充值并且继续迭代,通常4-6次迭代即可。
3.1.11 填充测试集中的缺失值
取决于测试集是否自带样品标签(分类属性)有两种方式可以用于缺失值替换。
- 如果测试集有标签,训练集中计算出的填充值直接用于测试集填充。
- 如果测试集没有标签,则测试集中的每个样品都重复
n_class次 (n_class为总的分类数)。第一次重复的样品设置其标签为class 1,并用class 1的对应值填充。第二次重复的样品设置其标签为class 2,并用class 2的对应值填充。
这个重复后的测试集用构建好的随机森林模型进行分类。在某个样品的所有重复中,获得最多分类的class则是该样品的标签,缺失值也根据对应class填充。
3.1.12 鉴定标签有误的样品
训练集通常是人为判断设定的标签。在一些领域,误标记会常出现。很多误标记的样本可以通过异常值检测的方式鉴定出。
3.1.13 鉴定异常样品
异常样本定义为需要从主数据集中移除的样本。从数据上来说,异常样品就是与其它所有样品相似性 (proximity)都很低的样品。通常为了缩小计算量,异常样品是从每个分类内部计算鉴定的。class j的一个异常样本就是在class j中某一个或多个与其它样本相似性很低的样本。
class j中的样品 n与class j中其它样品(k)的平均相似性定义为
\[ \overline{P}(n) = \sum_{class(k)=j}{}prox^2(n,k) \]
样品n是否为异常样品的度量方式为
\[ Raw\_Outlier(n) = \frac{num\_sample}{\overline{P}(n)} \]
如果平均相似度较低,这个度量值就会很高。计算这一组数据 (class j中每个样本 (J1, J2, Jn)与其它样本的平均相似度)的中位数和绝对偏差。每个平均相似度值减去中位数除以绝对偏差即获得最终的异常值度量标准。
\[ \begin{align} median &= median(\overline{P}(J_1), \overline{P}(J_2), ..., \overline{P}(J_n)) \\ mad &= \text{mad}(\overline{P}(J_1), \overline{P}(J_2), ..., \overline{P}(J_n)) \\ \overline{P}(J_1)_{scaled} &= \frac{\overline{P}(J_1)-median}{mad} \end{align} \]
3.1.14 无监督聚类
无监督聚类问题中,每个样品有一些度量值但都没有分类标签(分类问题)或响应变量(回归问题)。这类问题没有优化的标准,通常只能获得模糊的结论。最常见的应用是对数据进行聚类,能聚成几类,每一类是否意义明确。
在随机森林中,所有原始数据都视为来源于class 1, 然后构建一个相同大小的合成数据集都视为来源于class 2。第二个合成数据集通过对原始数据进行单变量 (univariate distribution)随机采样构建。合成数据集每个样品构建方式举例如下:
- 样品第一个变量的值从该变量在
n个样品中的值随机抽取一个。 - 样品第二个变量的值从该变量在
n个样品中的值随机抽取一个。 - 以此类推 (这就是做了一次样品内变量值的置换
permutation)
因此,Class 2数据有着独立的随机变量数据分布,并且每个变量的数据分布与原始矩阵的对应变量一致。Class 2数据打乱了原始数据的依赖结构。现在全体数据就有了两个分类,可以应用随机森林算法构建模型。
如果这两类数据的oob误分类率为40%或更高,说明随机森林the x -variables look too much like independent variables to random forests。变量的依赖在分组上贡献不大。如果误分类率低,则说明变量依赖发挥了重要作用。
把无标签数据集改造为包含两个分类的数据集给我们一些好处。缺失值可以有效填充。可以鉴定出异常样品。可以评估变量的重要性。可以做降维分析(如果原始数据有标签,非监督的降维 (`scaling)通常能保留下原始分类的结构)。最大的一个好处是使得聚类成为了可能。
3.1.15 平衡因类样品数目差别大带来的预测错误
在一些数据集,不同分类的预测错误是很不均衡的。一些类别预测错误率低,另一些类预测错误率高。这通常发生在每个类的样品数目差别较大时。随机森林试图最小化总错误率,默认保持大的类有较低的分类错误率,较小的类有较高的分类错误率。例如,在药物发现时,一个给定的分子会分类为有活性或无活性。通常分类为有活性的的概率为1/10或1/100。这时分类为有活性组的错误率就会很高。
用户可以通过输出每种分类的错误率作为预测不平衡性的评估。为了说明这个问题,我们采用一个有20个变量的合成数据集。class 1的数据符合一个球形的高斯分布,class 2的数据符合另一个球形高斯分布。训练集包含1000个class 1样品和50个class 2样品。测试集包括5000个class 1样品和250个class 2样品。
包含500棵树的随机森林输出的错误率为500 3.7 0.0 78.4。总体错误率较低(3.7%),但class 2的错误率高,为(78.4%)。可以通过对每个class设置不同的权重来平衡错误率。一个class的权重越高,它的分类错误率降低的就越多。一个常规的设置权重的方式是与class中样品数成反比。设置训练集中class 1的权重为1, class 2的权重为20,再次构建模型,输出为500 12.1 12.7 0.0。class 2的权重为20有点太高了,降低为10,获得结果如下500 4.3 4.2 5.2。
这样两个分类的错误率差不多平衡了。如果要求两个分类错误率相等,则还可以再微调class 2的权重。
需要注意的是,在平衡不同分类错误率时,总的错误率升高了。这是正常的。
3.1.16 检测新样品
对于测试集异常样品的检测可用来寻找新的不能分类于之前鉴定好的类中的样品。
以下面的卫星图像数据集做例子。训练集有4435个样品,测试集有2000个样品,36个变量,6个分组。
在测试集中,等间距的选取了5个样品。被选中样品的每个变量的值用从训练集中同一个变量的值随机选取一个替换。采用参数noutlier=2; nprox=1作为运行参数,输出下图:
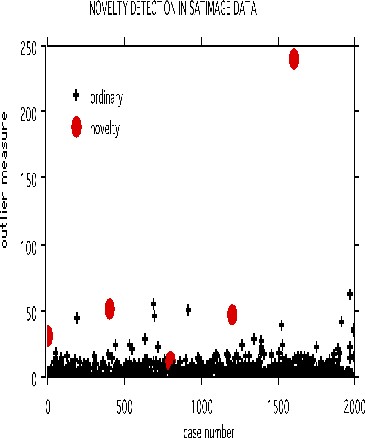
这展示了采用一个固定的训练集,可以检测测试集中的新样品。训练集构建的树可以存储起来用于检测后续的数据集。这个检测新样品的方法目前还处于试验阶段,还不能区分DNA检测中的新样本。
3.1.17 随机森林的短处
- 随机森林不能对全新的数据进行通用型判断。如一个冰淇淋1元钱,2个冰淇淋2元钱,3个冰淇淋3元钱,那么10个冰淇淋多少钱? 采用线性回归可以很快计算出,而随机森林则没有办法。
- 默认状态下随机森林会偏向样品数多的类。
3.2 随机森林实操
为了展示随机森林的能力,我们用一套早期的淋巴瘤基因表达芯片数据集,包含77个样品,2个分组和7070个变量 (基因或探针)。
3.2.1 数据格式和读入数据
输入数据为标准化之后的表达矩阵,基因在行,样本在列。随机森林对数值分布没有假设,每个基因表达值用于分类时是基因内部在不同样品直接比较,只要是样品之间标准化的数据即可,其他任何线性转换如log2,scale等都没有影响。
- 样品表达数据:DLBCL.expr.txt
- 样品分组信息:DLBCL.metadata.txt
expr_file <- "data/DLBCL.expr.txt"
metadata_file <- "data/DLBCL.metadata.txt"
# 每个基因表达值是内部比较,只要是样品之间标准化的数据即可,其它什么转换都关系不大
# 机器学习时,字符串还是默认为因子类型的好
expr_mat <- read.table(expr_file, row.names = 1, header = T, sep="\t", stringsAsFactors =T)
metadata <- read.table(metadata_file, row.names=1, header=T, sep="\t", stringsAsFactors =T)
dim(expr_mat)## [1] 7070 77基因表达表示例如下:
expr_mat[1:4,1:5]## DLBCL_1 DLBCL_2 DLBCL_3 DLBCL_4 DLBCL_5
## A28102 -1 25 73 267 16
## AB000114_at -45 -17 91 41 24
## AB000115_at 176 531 257 202 187
## AB000220_at 97 353 80 138 39Metadata表示例如下
head(metadata)## class
## DLBCL_1 DLBCL
## DLBCL_2 DLBCL
## DLBCL_3 DLBCL
## DLBCL_4 DLBCL
## DLBCL_5 DLBCL
## DLBCL_6 DLBCL3.2.2 样品筛选和排序
对读入的表达数据进行转置。通常我们是一行一个基因,一列一个样品。在构建模型时,数据通常是反过来的,一列一个基因,一行一个样品。每一列代表一个变量 (variable),每一行代表一个案例 (case)。这样更方便提取每个变量,且易于把模型中的x,y放到一个矩阵中。
样本表和表达表中的样本顺序对齐一致也是需要确保的一个操作。
# 表达数据转置
# 习惯上我们是一行一个基因,一列一个样品
# 做机器学习时,大部分数据都是反过来的,一列一个基因,一行一个样品
# 每一列代表一个变量
expr_mat <- t(expr_mat)
expr_mat_sampleL <- rownames(expr_mat)
metadata_sampleL <- rownames(metadata)
common_sampleL <- intersect(expr_mat_sampleL, metadata_sampleL)
# 保证表达表样品与METAdata样品顺序和数目完全一致
expr_mat <- expr_mat[common_sampleL,,drop=F]
metadata <- metadata[common_sampleL,,drop=F]3.2.3 判断是分类还是回归
前面读数据时已经给定了参数stringsAsFactors =T,这一步可以忽略了。
- 如果group对应的列为数字,转换为数值型 - 做回归
- 如果group对应的列为分组,转换为因子型 - 做分类
# R4.0之后默认读入的不是factor,需要做一个转换
# devtools::install_github("Tong-Chen/ImageGP")
library(ImageGP)
# 此处的class根据需要修改
group = "class"
# 如果group对应的列为数字,转换为数值型 - 做回归
# 如果group对应的列为分组,转换为因子型 - 做分类
if(numCheck(metadata[[group]])){
if (!is.numeric(metadata[[group]])) {
metadata[[group]] <- mixedToFloat(metadata[[group]])
}
} else{
metadata[[group]] <- as.factor(metadata[[group]])
}3.2.4 随机森林初步分析
library(randomForest)
# 查看参数是个好习惯
# 有了前面的基础概述,再看每个参数的含义就明确了很多
# 也知道该怎么调了
# 每个人要解决的问题不同,通常不是别人用什么参数,自己就跟着用什么参数
# 尤其是到下游分析时
# ?randomForest
# 查看源码
# randomForest:::randomForest.default加载包之后,直接分析一下,看到结果再调参。
# 设置随机数种子,具体含义见 https://mp.weixin.qq.com/s/6plxo-E8qCdlzCgN8E90zg
set.seed(304)
# 直接使用默认参数
rf <- randomForest(expr_mat, metadata[[group]])查看下初步结果, 随机森林类型判断为分类,构建了500棵树,每次决策时从随机选择的84个基因中做最优决策 (mtry),OOB估计的错误率是12.99%,挺高的。
分类效果评估矩阵Confusion matrix,显示DLBCL组的分类错误率为0.034,FL组的分类错误率为0.42。这是随机森林的默认操作,样本量多的分类错误率会低 (后面我们再调整)。
rf##
## Call:
## randomForest(x = expr_mat, y = metadata[[group]])
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 84
##
## OOB estimate of error rate: 12.99%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 56 2 0.03448276
## FL 8 11 0.421052633.2.5 随机森林参数调试 - 决策树的数目
增加决策树的数目到1000测试下分类率是否会降低。OOB估计的错误率是11.69%,还是不低。
分类效果评估矩阵Confusion matrix,显示DLBCL组的分类错误率为0.017 (略有降低。
),FL组的分类错误率为0.42 (依然较高)。
set.seed(304)
rf1000 <- randomForest(expr_mat, metadata[[group]], ntree=1000)
rf1000##
## Call:
## randomForest(x = expr_mat, y = metadata[[group]], ntree = 1000)
## Type of random forest: classification
## Number of trees: 1000
## No. of variables tried at each split: 84
##
## OOB estimate of error rate: 11.69%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 57 1 0.01724138
## FL 8 11 0.42105263增加决策树的数目到2000测试下分类率是否会降低。OOB估计的错误率是11.69%,与ntree=1000`时一致。
分类效果评估矩阵Confusion matrix,显示DLBCL组的分类错误率为0.017,FL组的分类错误率为0.42。FL组样品量少,分类效果还是不好。
set.seed(304)
rf2000 <- randomForest(expr_mat, metadata[[group]], ntree=2000)
rf2000##
## Call:
## randomForest(x = expr_mat, y = metadata[[group]], ntree = 2000)
## Type of random forest: classification
## Number of trees: 2000
## No. of variables tried at each split: 84
##
## OOB estimate of error rate: 11.69%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 57 1 0.01724138
## FL 8 11 0.42105263绘制下从第1到2000棵树时,OOB的变化趋势是怎样的?从这张图可以看到,600棵树之后,基本没有影响了。
library(ggplot2)
ImageGP::sp_lines(as.data.frame(rf2000$err.rate), manual_color_vector="Set2",
x_label="Number of trees", y_label="Error rate",line_size=0.6,
width=6, height=4
)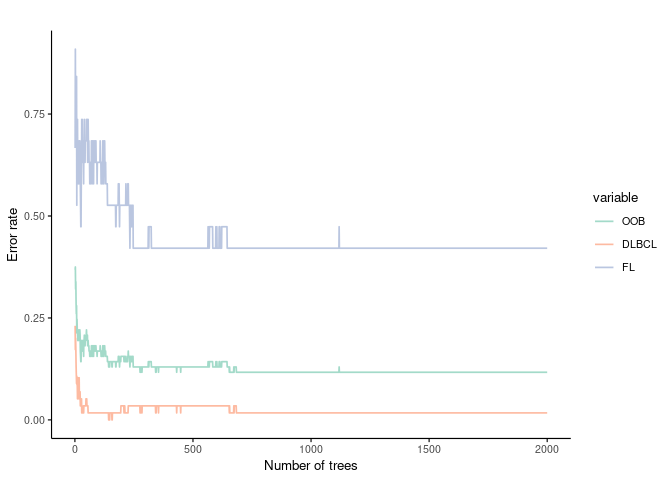
Figure 3.1: 第1到2000棵树时,OOB的变化趋势
3.2.6 随机森林参数调试 - 用于决策的变量的数目 (m)
影响随机森林的第二个参数(m): 构建每棵决策树时随机抽取的变量的数目。在randomForest函数中有一个参数mtry即是做这个的。在处理分类问题时,其默认值为sqrt(p);处理回归问题时,其默认值为p/3;p是总的变量数目。
我们先人工测试几个不同的mtry看下效果。mtry=20时错误率为15.58%。
# 增加树的数目没有给出好的结果,这里还是用的默认的500棵树以便获得较快的运行速度
set.seed(304)
rf_mtry20 <- randomForest(expr_mat, metadata[[group]], mtry=20)
rf_mtry20##
## Call:
## randomForest(x = expr_mat, y = metadata[[group]], mtry = 20)
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 20
##
## OOB estimate of error rate: 15.58%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 57 1 0.01724138
## FL 11 8 0.57894737我们先人工测试几个不同的mtry看下效果。mtry=50时错误率为11.69% (默认使用了84个变量,准确率为12.99%)。
# 增加树的数目没有给出好的结果,这里还是用的默认的500棵树以便获得较快的运行速度
set.seed(304)
rf_mtry50 <- randomForest(expr_mat, metadata[[group]], mtry=50)
rf_mtry50##
## Call:
## randomForest(x = expr_mat, y = metadata[[group]], mtry = 50)
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 50
##
## OOB estimate of error rate: 11.69%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 57 1 0.01724138
## FL 8 11 0.42105263我们先人工测试几个不同的mtry看下效果。mtry=100时错误率为11.69%。
# 增加树的数目没有给出好的结果,这里还是用的默认的500棵树以便获得较快的运行速度
set.seed(304)
rf_mtry100 <- randomForest(expr_mat, metadata[[group]], mtry=100)
rf_mtry100##
## Call:
## randomForest(x = expr_mat, y = metadata[[group]], mtry = 100)
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 100
##
## OOB estimate of error rate: 11.69%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 57 1 0.01724138
## FL 8 11 0.42105263一个个测试也不是办法,tuneRF给我们提供了一个根据OOB值迭代鉴定最合适的mtry值的函数。(测试几次,不太好用,每调整一次stepfactor,结果变化很大)
# mtryStart: 从多少个变量开始尝试,可用默认值。程序会自动向更多变量或更少变量迭代。
# ntreeTry: 迭代时构建多少棵树,这里设置为500,与我们上面获得的效果比较好的树一致。
# stepFactor: 迭代步长,mtryStart向更多变量迭代时乘以此值;mtryStart向更少变量迭代时除以此值。
# improve:如果迭代不能给OOB带来给定值的改善,则停止迭代。
set.seed(304)
tuneRF(expr_mat, metadata[[group]], ntreeTry=500, stepFactor=1.5, improve=1e-5)## mtry = 84 OOB error = 12.99%
## Searching left ...
## mtry = 56 OOB error = 12.99%
## 0 1e-05
## Searching right ...
## mtry = 126 OOB error = 10.39%
## 0.2 1e-05
## mtry = 189 OOB error = 10.39%
## 0 1e-05## mtry OOBError
## 56.OOB 56 0.1298701
## 84.OOB 84 0.1298701
## 126.OOB 126 0.1038961
## 189.OOB 189 0.1038961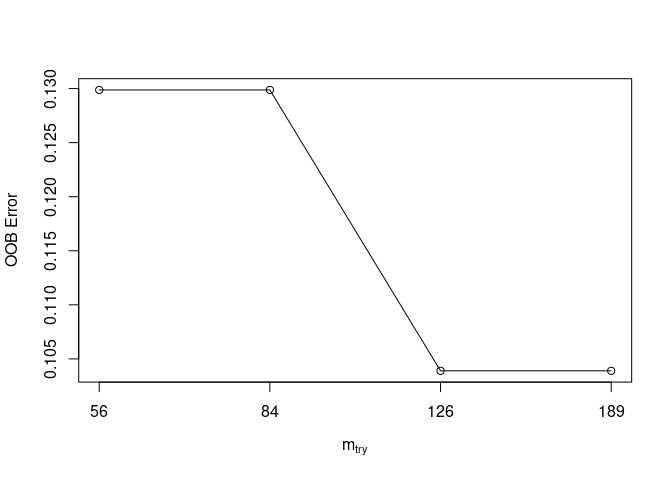
Figure 3.2: tuneRF根据OOB值迭代鉴定最合适的mtry值
3.2.7 RandomFOorest 自带工具的调参
randomForest自带了另一个函数rfcv,通过嵌套交叉验证方式评估了根据变量重要性减少预测变量后的模型的性能。
rfcv先用所有变量运行一次随机森林计算,评估每个变量对分类模型的重要性。然后根据设定的step选择一系列对分类模型贡献最大的变量再次构建模型并使用K-fold交叉验证评估每个模型的性能,输出如下结果:
set.seed(304)
result = rfcv(expr_mat, metadata[[group]], cv.fold=10)
result$error.cv
# 7070 3535 1768 884 442 221 110 55
# 0.11688312 0.11688312 0.11688312 0.07792208 0.11688312 0.09090909 0.09090909 0.09090909
# 28 14 7 3 1
# 0.10389610 0.12987013 0.07792208 0.14285714 0.18181818 从上面结果来看,使用7个贡献最大的变量构建随机森林时错误率最低。
这与后面基于变量迭代选择 (RFE)算法进行关键变量筛选和确定关键变量数目对模型的影响是一致的。
# 使用replicate函数进行多次交叉验证
result= replicate(5, rfcv(expr_mat, metadata[[group]], cv.fold=10), simplify=F)
error.cv= sapply(result, "[[", "error.cv")3.3 随机森林的 10 折交叉验证代码
除了 OOB,我们还可以怎么评估模型的准确性呢?这里没有测试集,那么就拿原始数据做个评估吧(注意:这样会低估预测错误率):
# 查看模型的类,为randomForest
class(rf1000)## [1] "randomForest"# 查看 predict 函数的帮助,默认帮助信息为通用函数 predict
# ?predict
# 查看 randomForest 类的 predict 的帮助(predict+'.'+类名字)
# 像 print 此类函数,也是如此查看帮助或源码
# type 参数: response 表示返回分类的值; prob 表示分类的概率;vote 表示 vote counts
# ?predict.randomForest3.3.1 precit函数的应用
开始预测
preds <- predict(rf1000, expr_mat, type="response")查看下preds对象,显示的是每个样品被预测为属于什么类。
preds## DLBCL_1 DLBCL_2 DLBCL_3 DLBCL_4 DLBCL_5 DLBCL_6 DLBCL_7 DLBCL_8
## DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL
## DLBCL_9 DLBCL_10 DLBCL_11 DLBCL_12 DLBCL_13 DLBCL_14 DLBCL_15 DLBCL_16
## DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL
## DLBCL_17 DLBCL_18 DLBCL_19 DLBCL_20 DLBCL_21 DLBCL_22 DLBCL_23 DLBCL_24
## DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL
## DLBCL_25 DLBCL_26 DLBCL_27 DLBCL_28 DLBCL_29 DLBCL_30 DLBCL_31 DLBCL_32
## DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL
## DLBCL_33 DLBCL_34 DLBCL_35 DLBCL_36 DLBCL_37 DLBCL_38 DLBCL_39 DLBCL_40
## DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL
## DLBCL_41 DLBCL_42 DLBCL_43 DLBCL_44 DLBCL_45 DLBCL_46 DLBCL_47 DLBCL_48
## DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL
## DLBCL_49 DLBCL_50 DLBCL_51 DLBCL_52 DLBCL_53 DLBCL_54 DLBCL_55 DLBCL_56
## DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL DLBCL
## DLBCL_57 DLBCL_58 FL_1 FL_2 FL_3 FL_4 FL_5 FL_6
## DLBCL DLBCL FL FL FL FL FL FL
## FL_7 FL_8 FL_9 FL_10 FL_11 FL_12 FL_13 FL_14
## FL FL FL FL FL FL FL FL
## FL_15 FL_16 FL_17 FL_18 FL_19
## FL FL FL FL FL
## Levels: DLBCL FL计算模型效果评估矩阵(也称混淆矩阵)。从矩阵可以看出敏感性、特异性都是 100%。完美的模型!!!(这里主要是看下predict如何使用,完美的模型只是说训练的完美,不能表示预测性能的完美(还有可能是过拟合),因为没有用独立数据集进行评估。)
library(caret)
caret::confusionMatrix(preds, metadata[[group]])## Confusion Matrix and Statistics
##
## Reference
## Prediction DLBCL FL
## DLBCL 58 0
## FL 0 19
##
## Accuracy : 1
## 95% CI : (0.9532, 1)
## No Information Rate : 0.7532
## P-Value [Acc > NIR] : 3.343e-10
##
## Kappa : 1
##
## Mcnemar's Test P-Value : NA
##
## Sensitivity : 1.0000
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 1.0000
## Prevalence : 0.7532
## Detection Rate : 0.7532
## Detection Prevalence : 0.7532
## Balanced Accuracy : 1.0000
##
## 'Positive' Class : DLBCL
## predict还可以返回分类的概率 (有了这个是不是就可以绘制 ROC 曲线和计算 AUC 值了)。
preds_prob <- predict(rf1000, expr_mat, type="prob")
head(preds_prob)## DLBCL FL
## DLBCL_1 0.951 0.049
## DLBCL_2 0.972 0.028
## DLBCL_3 0.975 0.025
## DLBCL_4 0.984 0.016
## DLBCL_5 0.963 0.037
## DLBCL_6 0.989 0.011predict还可以返回分类的vote值。
preds_prob <- predict(rf1000, expr_mat, type="vote")
head(preds_prob)3.3.2 基于predict结果绘制ROC曲线
直接绘制
library(ROCR)
pred.obj <- prediction (preds_prob[,1], metadata[[group]])
ROC.perf <- performance(pred.obj, "fpr","tpr")
plot(ROC.perf)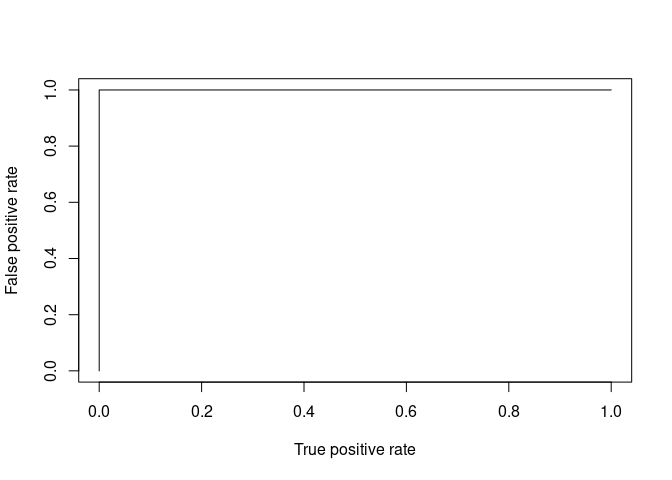
整理数据用ggplot2绘制。
ROC.perf.df <- data.frame(FPR=ROC.perf@x.values[[1]], TPR=ROC.perf@y.values[[1]])
library(ggplot2)
ggplot(ROC.perf.df, aes(x=FPR, y=TPR, group=1)) + geom_step(direction="vh", color='red') +
geom_abline(intercept = 0, slope = 1) + theme_classic() +
scale_y_continuous(expand=c(0,0)) +
xlab("False positive rate") + ylab("True positive rate") + coord_fixed(1)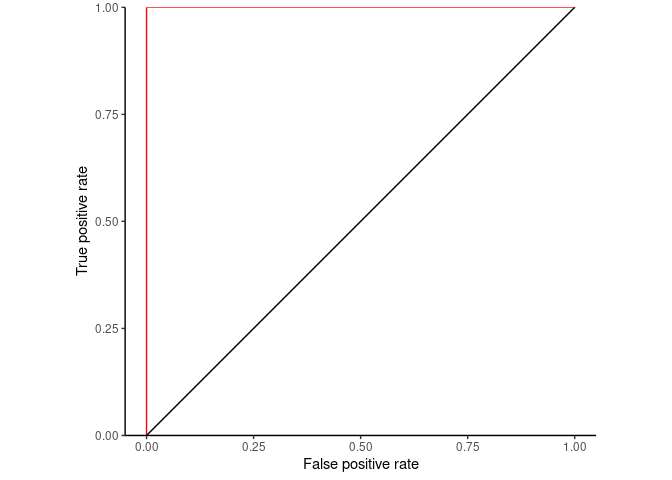
ROC曲线的显著性 (AUC是否显著大于0.5)
library(verification)
# The p-value produced is related to the Mann-Whitney U statistics.
# The p-value is calculated using the wilcox.test function which
# automatically handles ties and makes approximations for large values.
# The p-value addresses the null hypothesis $H_o:$
# The area under the ROC curve is 0.5 i.e. the forecast has no skill.
# ?roc.area
# https://stats.stackexchange.com/questions/75050/in-r-how-to-compute-the-p-value-for-area-under-roc
roc.area(as.numeric(metadata[[group]]=="DLBCL"), preds_prob)3.3.3 随机森林的 10 折交叉验证代码
前面主要是学习下predict和confusionMatrix函数的使用。把前面的代码串起来,就构成了一个随机森林的 10 折交叉验证代码:
# https://stackoverflow.com/questions/47960427/how-to-calculate-the-oob-of-random-forest
K = 10
m = nrow(expr_mat)
set.seed(1)
# 构建K-fold数据集
kfold <- sample(rep(1:K, length.out=m), size=m, replace=F)
# 包装下randomForest函数,增加预测部分
randomForestCV <- function(x, y, xtest, ytest, type="response", seed=1, ...){
set.seed(seed)
model <- randomForest(x, y, ...)
preds <- predict(model, xtest, type=type)
return(data.frame(preds, real=ytest))
}
# 交叉训练和评估
CV_rf <- lapply(1:K, function(x, ...){
train_set = expr_mat[kfold != x,]
train_label = metadata[[group]][kfold!=x]
validate_set = expr_mat[kfold == x,]
validate_label = metadata[[group]][kfold==x]
randomForestCV(x=train_set, y=train_label, xtest=validate_set, ytest=validate_label, ...)
})
kfold_estimate <- do.call(rbind, CV_rf)查看下10 折交叉验证的预测结果
kfold_estimate## preds real
## DLBCL_3 DLBCL DLBCL
## DLBCL_8 DLBCL DLBCL
## DLBCL_9 DLBCL DLBCL
## DLBCL_35 DLBCL DLBCL
## DLBCL_57 DLBCL DLBCL
## FL_9 DLBCL FL
## FL_10 DLBCL FL
## FL_18 FL FL
## DLBCL_15 DLBCL DLBCL
## DLBCL_16 DLBCL DLBCL
## DLBCL_40 DLBCL DLBCL
## DLBCL_41 DLBCL DLBCL
## DLBCL_42 DLBCL DLBCL
## DLBCL_44 DLBCL DLBCL
## DLBCL_51 DLBCL DLBCL
## DLBCL_53 DLBCL DLBCL
## DLBCL_5 DLBCL DLBCL
## DLBCL_20 DLBCL DLBCL
## DLBCL_25 DLBCL DLBCL
## DLBCL_32 DLBCL DLBCL
## DLBCL_38 DLBCL DLBCL
## FL_2 DLBCL FL
## FL_12 DLBCL FL
## FL_16 FL FL
## DLBCL_4 DLBCL DLBCL
## DLBCL_6 DLBCL DLBCL
## DLBCL_10 DLBCL DLBCL
## DLBCL_14 DLBCL DLBCL
## DLBCL_18 DLBCL DLBCL
## DLBCL_39 DLBCL DLBCL
## FL_1 DLBCL FL
## FL_6 FL FL
## DLBCL_17 DLBCL DLBCL
## DLBCL_19 DLBCL DLBCL
## DLBCL_22 DLBCL DLBCL
## DLBCL_33 DLBCL DLBCL
## DLBCL_36 DLBCL DLBCL
## DLBCL_45 DLBCL DLBCL
## DLBCL_47 DLBCL DLBCL
## FL_11 DLBCL FL
## DLBCL_13 DLBCL DLBCL
## DLBCL_23 DLBCL DLBCL
## DLBCL_37 DLBCL DLBCL
## DLBCL_52 DLBCL DLBCL
## FL_3 FL FL
## FL_5 FL FL
## FL_17 DLBCL FL
## FL_19 FL FL
## DLBCL_11 DLBCL DLBCL
## DLBCL_12 DLBCL DLBCL
## DLBCL_27 DLBCL DLBCL
## DLBCL_28 DLBCL DLBCL
## DLBCL_54 DLBCL DLBCL
## DLBCL_56 DLBCL DLBCL
## DLBCL_58 DLBCL DLBCL
## FL_14 DLBCL FL
## DLBCL_1 DLBCL DLBCL
## DLBCL_26 FL DLBCL
## DLBCL_29 FL DLBCL
## DLBCL_43 DLBCL DLBCL
## DLBCL_50 DLBCL DLBCL
## FL_8 DLBCL FL
## FL_15 FL FL
## DLBCL_2 DLBCL DLBCL
## DLBCL_7 DLBCL DLBCL
## DLBCL_48 DLBCL DLBCL
## DLBCL_55 DLBCL DLBCL
## FL_4 FL FL
## FL_7 FL FL
## FL_13 FL FL
## DLBCL_21 DLBCL DLBCL
## DLBCL_24 DLBCL DLBCL
## DLBCL_30 DLBCL DLBCL
## DLBCL_31 DLBCL DLBCL
## DLBCL_34 DLBCL DLBCL
## DLBCL_46 DLBCL DLBCL
## DLBCL_49 DLBCL DLBCL计算模型效果评估矩阵(也称混淆矩阵)。准确性值为0.8581,OOB 的错误率是88.31%,相差不大。但Kappa值不算高0.5614,这也是数据集中两个分组的样本数目不均衡导致的。
library(caret)
caret::confusionMatrix(kfold_estimate$preds, kfold_estimate$real)## Confusion Matrix and Statistics
##
## Reference
## Prediction DLBCL FL
## DLBCL 56 9
## FL 2 10
##
## Accuracy : 0.8571
## 95% CI : (0.7587, 0.9265)
## No Information Rate : 0.7532
## P-Value [Acc > NIR] : 0.01936
##
## Kappa : 0.5614
##
## Mcnemar's Test P-Value : 0.07044
##
## Sensitivity : 0.9655
## Specificity : 0.5263
## Pos Pred Value : 0.8615
## Neg Pred Value : 0.8333
## Prevalence : 0.7532
## Detection Rate : 0.7273
## Detection Prevalence : 0.8442
## Balanced Accuracy : 0.7459
##
## 'Positive' Class : DLBCL
## # 结果如下相关指标前面大都有讲述或?confusionMatrix可看到对应的计算公式。
前面只是简单的展示如何进行的K-fold评估,但没有进行调参。主要是理解K-fold的操作理念。
3.4 基于Caret进行随机森林调参
Caret是R中一个试图流程化机器学习方法的包,其具体应用会在第4章介绍 (建议先阅读第4章)。
3.4.1 基于Caret进行随机森林随机调参
Caret只给randomForest函数提供了一个可调节参数mtry,即决策时的变量数目。随机调参就是函数会随机选取一些符合条件的参数值,逐个去尝试哪个可以获得更好的效果。
tuneLnegth设置随机选取的参数值的数目。metric设置模型评估标准,分类问题用Accuracy和Kappa值。也可以设置ROC (在第4章caret部分有讲解)。
# 这个步骤运行较慢
# 为了方便,每次结果都先存储了下来,实际自己使用时可以忽略。
if(file.exists('rda/rf_random.rda')){
rf_random <- readRDS("rda/rf_random.rda")
} else {
# Create model with default parameters
# search="random":随机搜索
trControl <- trainControl(method="repeatedcv", number=10, repeats=3, search="random")
# 设置随机数种子,使得结果可重复
seed <- 1
set.seed(seed)
rf_random <- train(x=expr_mat, y=metadata[[group]], method="rf",
tuneLength = 15, # 随机15个参数值或参数值组合
metric="Accuracy", #metric='Kappa'
trControl=trControl)
saveRDS(rf_random, "rda/rf_random.rda")
}
print(rf_random)## Random Forest
##
## 77 samples
## 7070 predictors
## 2 classes: 'DLBCL', 'FL'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 70, 69, 69, 70, 69, 69, ...
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa
## 270 0.8988095 0.6586786
## 330 0.8821429 0.6129643
## 597 0.8946429 0.6529643
## 1301 0.9077381 0.7020960
## 1533 0.8988095 0.6729643
## 2177 0.9119048 0.7154293
## 2347 0.8904762 0.6462976
## 3379 0.8898810 0.6379783
## 4050 0.8940476 0.6475021
## 4065 0.8904762 0.6469326
## 4567 0.8946429 0.6564564
## 4775 0.8815476 0.6202005
## 5026 0.8946429 0.6709195
## 5307 0.8857143 0.6297244
## 6070 0.8815476 0.6163910
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 2177.最佳模型是mtry = 2177。
3.4.1.1 基于Caret进行随机森林指定参数调参
使用tuneGrid指定需要调整的参数和参数值,参数名字需要与函数预留的调参参数名字一致。
# 这个步骤运行较慢
# 为了方便,每次结果都先存储了下来,实际自己使用时可以忽略。
if(file.exists('rda/rf_grid.rda')){
rf_grid <- readRDS("rda/rf_grid.rda")
} else {
# Create model with default parameters
trControl <- trainControl(method="repeatedcv", number=10, repeats=3, search="grid")
# 根据经验或感觉设置一些待查询的参数和参数值
tuneGrid <- expand.grid(mtry=c(3,10,20,50,100,300,700,1000,2000))
# 设置随机数种子,使得结果可重复
seed <- 1
set.seed(seed)
rf_grid <- train(x=expr_mat, y=metadata[[group]], method="rf",
tuneGrid = tuneGrid, #
metric="Accuracy", #metric='Kappa'
trControl=trControl)
saveRDS(rf_grid, "rda/rf_grid.rda")
}
print(rf_grid)## Random Forest
##
## 77 samples
## 7070 predictors
## 2 classes: 'DLBCL', 'FL'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 70, 69, 69, 70, 69, 69, ...
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa
## 3 0.7875000 0.1596078
## 10 0.8345238 0.3766667
## 20 0.8511905 0.4731884
## 50 0.8648810 0.5324041
## 100 0.8779762 0.5920119
## 300 0.8946429 0.6558215
## 700 0.9071429 0.7002659
## 1000 0.9029762 0.6824881
## 2000 0.9071429 0.6920119
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 700.最佳模型是mtry = 700。
3.4.1.2 调整Caret没有提供的参数
如果我们想调整的参数Caret没有提供,可以用下面的方式自己手动+Caret配合调参。
# 这个步骤运行较慢
# 为了方便,每次结果都先存储了下来,实际自己使用时可以忽略。
if(file.exists('rda/rf_manual.rda')){
results <- readRDS("rda/rf_manual.rda")
} else {
# Manual Search
trControl <- trainControl(method="repeatedcv", number=10, repeats=3, search="grid")
# 用默认值固定mtry
# tunegrid <- expand.grid(mtry=c(sqrt(ncol(expr_mat))))
tunegrid <- expand.grid(mtry=c(700))
# 定义模型列表,存储每一个模型评估结果
modellist <- list()
# 调整的参数是决策树的数量
for (ntree in c(500,700, 800, 1000)) {
set.seed(seed)
fit <- train(x=expr_mat, y=metadata[[group]], method="rf",
metric="Accuracy", tuneGrid=tunegrid,
trControl=trControl, ntree=ntree)
key <- toString(ntree)
modellist[[key]] <- fit
}
# compare results
results <- resamples(modellist)
saveRDS(results, "rda/rf_manual.rda")
}
summary(results)##
## Call:
## summary.resamples(object = results)
##
## Models: 500, 700, 800, 1000
## Number of resamples: 30
##
## Accuracy
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 500 0.5714286 0.875 0.9375 0.9071429 1 1 0
## 700 0.5714286 0.875 0.9375 0.9071429 1 1 0
## 800 0.5714286 0.875 1.0000 0.9154762 1 1 0
## 1000 0.5714286 0.875 1.0000 0.9113095 1 1 0
##
## Kappa
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 500 -0.2352941 0.6 0.8571429 0.7002659 1 1 0
## 700 -0.2352941 0.6 0.8571429 0.7002659 1 1 0
## 800 -0.2352941 0.6 1.0000000 0.7269326 1 1 0
## 1000 -0.2352941 0.6 1.0000000 0.7091548 1 1 0绘制下图形
dotplot(results)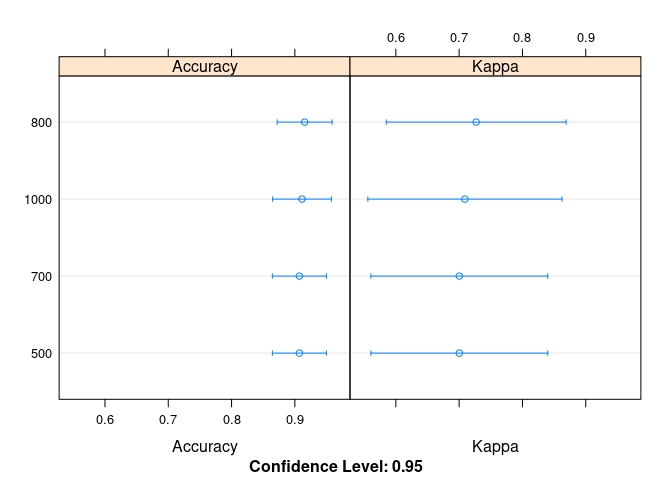
Figure 3.3: 700棵树时效果最好
3.4.1.3 扩展Caret
如果我们想调整的参数Caret没有提供,另一个方式是重新定义一个方法。尤其是参数比较多时,自己写循环会比较乱。
rf方法在Caret中的定义可通过此链接查看https://github.com/topepo/caret/blob/master/models/files/rf.R。需要做的修改就是在parameters上增加一个参数 (ntree),fit时调用下这个参数 (param$ntree)。
定义新方法
# https://machinelearningmastery.com/tune-machine-learning-algorithms-in-r/
customRF <- list(type = "Classification", library = "randomForest", loop = NULL,
parameters = data.frame(parameter = c("mtry", "ntree"),
class = rep("numeric", 2),
label = c("mtry", "ntree")),
# grid也可以不定义,直接在函数中传过来就行
grid = function(x, y, len = NULL, search = "grid") {
if(search == "grid") {
out <- expand.grid(mtry = caret::var_seq(p = ncol(x),
classification = is.factor(y),
len = len),
ntree = c(500,700,900,1000,1500))
} else {
out <- data.frame(mtry = unique(sample(1:ncol(x), size = len, replace = TRUE)),
ntree = unique(sample(c(500,700,900,1000,1500),
size = len, replace = TRUE)))
}
},
fit = function(x, y, wts, param, lev, last, weights, classProbs, ...) {
randomForest(x, y, mtry = param$mtry, ntree=param$ntree, ...)
},
predict = function(modelFit, newdata, preProc = NULL, submodels = NULL)
predict(modelFit, newdata),
prob = function(modelFit, newdata, preProc = NULL, submodels = NULL)
predict(modelFit, newdata, type = "prob"),
sort = function(x) x[order(x[,1]),],
levels = function(x) x$classes
)调用新方法
# train model
if(file.exists('rda/rf_custom.rda')){
rf_custom <- readRDS("rda/rf_custom.rda")
} else {
trControl <- trainControl(method="repeatedcv", number=10, repeats=3)
tunegrid <- expand.grid(mtry=c(3,10,20,50,100,300,700,1000,2000),
ntree=c(500,700, 800, 1000, 1500, 2000))
set.seed(1)
rf_custom <- train(x=expr_mat, y=metadata[[group]], method=customRF,
metric="Accuracy", tuneGrid=tunegrid,
trControl=trControl)
saveRDS(rf_custom, "rda/rf_custom.rda")
}
print(rf_custom)## 77 samples
## 7070 predictors
## 2 classes: 'DLBCL', 'FL'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 70, 69, 69, 70, 69, 69, ...
## Resampling results across tuning parameters:
##
## mtry ntree Accuracy Kappa
## 3 500 0.7964286 0.1925490
## 3 700 0.7964286 0.1925490
## 3 800 0.7964286 0.1925490
## 3 1000 0.7922619 0.1792157
## 3 1500 0.7964286 0.1992157
## 3 2000 0.7922619 0.1792157
## 10 500 0.8083333 0.3000000
## 10 700 0.8220238 0.3233333
## 10 800 0.8214286 0.3225490
## 10 1000 0.8351190 0.3796078
## 10 1500 0.8303571 0.3566667
## 10 2000 0.8220238 0.3366667
## 20 500 0.8660714 0.5162745
## 20 700 0.8523810 0.4696078
## 20 800 0.8571429 0.4927962
## 20 1000 0.8351190 0.4061296
## 20 1500 0.8565476 0.4924041
## 20 2000 0.8517857 0.4727962
## 50 500 0.8744048 0.5531884
## 50 700 0.8648810 0.5428803
## 50 800 0.8702381 0.5465217
## 50 1000 0.8702381 0.5398551
## 50 1500 0.8702381 0.5398551
## 50 2000 0.8702381 0.5398551
## 100 500 0.8779762 0.5958215
## 100 700 0.8821429 0.6053453
## 100 800 0.8821429 0.5986786
## 100 1000 0.8952381 0.6398551
## 100 1500 0.8779762 0.5920119
## 100 2000 0.8869048 0.6131884
## 300 500 0.9029762 0.6720119
## 300 700 0.9029762 0.6758215
## 300 800 0.9071429 0.6920119
## 300 1000 0.8946429 0.6491548
## 300 1500 0.8988095 0.6624881
## 300 2000 0.8988095 0.6691548
## 700 500 0.9107143 0.7046450
## 700 700 0.9113095 0.7091548
## 700 800 0.9029762 0.6862976
## 700 1000 0.9071429 0.6920119
## 700 1500 0.9029762 0.6824881
## 700 2000 0.9071429 0.6958215
## 1000 500 0.9113095 0.7091548
## 1000 700 0.9029762 0.6824881
## 1000 800 0.9071429 0.6891548
## 1000 1000 0.9077381 0.7020960
## 1000 1500 0.9029762 0.6824881
## 1000 2000 0.9071429 0.6958215
## 2000 500 0.9029762 0.6824881
## 2000 700 0.9029762 0.6824881
## 2000 800 0.9119048 0.7116198
## 2000 1000 0.9029762 0.6824881
## 2000 1500 0.9029762 0.6824881
## 2000 2000 0.8988095 0.6691548
##
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were mtry = 2000 and ntree = 800.绘制一张分布图
plot(rf_custom)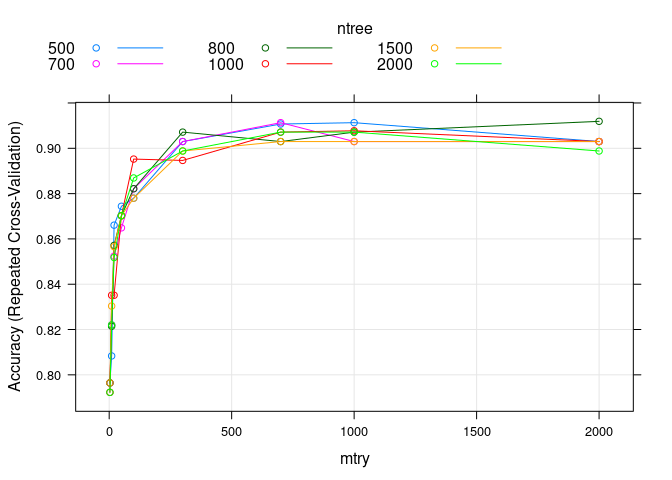
Figure 3.4: 同时评估mtry和ntree
3.4.2 随机森林变量选择
- lasso on random forest https://stats.stackexchange.com/questions/52034/using-lasso-on-random-forest?rq=1
https://www.huaweicloud.com/articles/b96eaee4bc2ffa206df22ce8abaee332.html
dlblc <- read.table("DLBCL.tab", row.names = NULL, header=T)
dim(dlblc)class = dlblc$class
table(class)metadata = data.frame(sample=c(paste("DLBCL", 1:58, sep="_"),
paste("FL", 1:19, sep="_")),
class=class)
head(metadata)
write.table(metadata, "dlbcl.metadata.txt", sep="\t", row.names=F, col.names = T, quote=F)rownames(dlblc) <- metadata$sample
dlblc <- dlblc[,1:7070]
dlblc <- t(dlblc)
dlblc[1:3,1:4]
library(ImageGP)
sp_writeTable(dlblc, file="dlblc.expr.txt", keep_rownames = T)3.4.3 从Bagging到随机森林
Bagging决策树只有一个参数,取多少棵树,t。
随机森林还有第二个参数,每次构建决策树时使用多少变量。我们上面的数据集只有2个变量 (x, y),没什么可选的。但常见数据集都有很多变量,如基因表达表中每个基因就是一个变量,OTU丰度表中每个OTU就是一个变量。
假设我们的数据集有p个变量。每次构建决策树时通常随机抽取m (m<<p)个变量进行每个节点决策变量的选择,m通常为\(\sqrt{p}\)或\(\frac{p}{3}\)。
之所以这么做,是为了使得每个构建的树存在一些随机性,也降低了不同树之间的关联,可以从整体上提高随机森林算法的性能。这通常也称为特征聚合 (feature bagging)。
data <- as.data.frame(matrix(rnorm(120), nrow=10))
colnames(data) <- paste0("Gene_",1:12)
rownames(data) <- paste0("Sample_",1:10)
sampleL <- rownames(data)
variableL <- colnames(data)
data[1:3,1:3]data[sample(sampleL, 10, replace=T),]3.4.4 Bootstrap小样品
Bootstrap resampling is not a cure for small samples. If you have just twenty four observations in your dataset, then each of the samples taken with replacement from this data would consist of not more than the twenty four distinct values. Shuffling the cases and not drawing some of them would not change much about your ability to learn anything new about the underlying distribution. So a small sample is a problem for bootstrap.
Decision trees are trained by splitting the data conditionally on the predictor variables, one variable at a time, to find such subsamples that have greatest discriminatory power. If you have only twenty four cases, then say that if you were lucky and all the splits were even in size, then with two splits you would end up with four groups of six cases, with tree splits, with eight groups of three. If you calculated conditional means on the samples (to predict continuous values in regression trees, or conditional probabilities in decision trees), you would base your conclusion only on those few cases! So the sub-samples that you would use to make the decisions would be even smaller than your original data.
Faster random forest
Awesome random forest
RandomForest iphnotebook
library(rpart)
library(rpart.plot)
library(rattle)
fit <- rpart(color ~ x, data = data)
fancyRpartPlot(fit)
plot(fit, branch = 1)3.5 参考
很细致的理论教程 https://www.listendata.com/2014/11/random-forest-with-r.html
很细致的理论教程 https://towardsdatascience.com/understanding-random-forest-58381e0602d2
随机森林作者教程 https://www.stat.berkeley.edu/~breiman/RandomForests/reg_philosophy.html
数据集大小的讨论 https://stats.stackexchange.com/questions/192310/is-random-forest-suitable-for-very-small-data-sets
Bootstrap小样品 https://stats.stackexchange.com/questions/112147/can-bootstrap-be-seen-as-a-cure-for-the-small-sample-size
https://medium.com/@williamkoehrsen/random-forest-simple-explanation-377895a60d2d
很好的网站 https://machinelearningmastery.com/tune-machine-learning-algorithms-in-r/
很好的网站 https://machinelearningmastery.com/random-forest-ensemble-in-python/
https://www.blopig.com/blog/2017/04/a-very-basic-introduction-to-random-forests-using-r/
引用最多的RandomForest文献 https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-7-3
RandomForest生物中的应用 https://www.sciencedirect.com/science/article/pii/S0888754312000626
RandomForests in python https://towardsdatascience.com/random-forest-in-python-24d0893d51c0
https://baike.baidu.com/item/%E9%9A%8F%E6%9C%BA%E6%A3%AE%E6%9E%97/1974765?fr=aladdin
3.5.1 随机森林平衡样本
前面无论是用全部变量还是筛选出的特征变量、无论如何十折交叉验证调参,获得的模型应用于测试集时虽然预测准确率能在90%以上,但与不基于任何信息的随机猜测相比,这个模型都是统计不显著的。对于这种非平衡数据集,模型整体的预测准确率也不是好的评估指标。一个原因应该是样本不平衡导致的。DLBCL组的样品数目约为FL组的3倍。不通过建模而只是盲猜结果为DLBCL即可获得75%的正确率。
如何处理非平衡样品是每一个算法应用于分类问题时都需要考虑的。
不平衡样本在模型构建中的影响主要体现在2个地方:
- 随机采样构建决策树时会有较大概率只拿到了样品多的分类,这些树将没有能力预测样品少的分类,从而构成无意义的决策树。
- 在决策树的每个分子节点所做的决策会倾向于整体分类纯度,因此样品少的分类对结果的贡献和影响少,更不容易分类正确。
一般处理方式有下面4种:
- Class weights: 样品少的类分类错误给予更高的罚分 (impose a heavier cost when errors are made in the minority class)
- Down-sampling: 从样品多的类随机移除样品
- Up-sampling: 在样品少的类随机复制样品 (randomly replicate instances in the minority class)
- Synthetic minority sampling technique (SMOTE): 通过插值在样品少的类中合成填充样本
这些分类加权或采样技术对阈值依赖的评估指标如准确性等影响较大,它们相当于把决策阈值推向了ROC曲线中的”最优位置” (这在第5章:Boruta特征变量筛选部分有讲)。但这些权重加权或采样技术对ROC曲线通常影响不会太大。
3.5.1.1 基于模拟数据的样本不平衡处理
这里先通过一套模拟数据熟悉下处理流程,再应用于真实数据。采用caret包的twoClassSim函数生成包含20个有意义变量和10个噪音变量的数据集。该数据集包含5000个观察样品,分为两组,多数组和少数组的样品数目比例为50:1 (通过intercept参数控制)。
library(dplyr) # for data manipulation
library(caret) # for model-building
# install.packages("xts")
# install.packages("quantmod")
# wget https://cran.r-project.org/src/contrib/Archive/DMwR/DMwR_0.4.1.tar.gz
# R CMD INSTALL DMwR_0.4.1.tar.gz
library(DMwR) # for smote implementation
# 或使用smotefamily代替
# library(smotefamily) # for smote implementation
library(purrr) # for functional programming (map)
library(pROC) # for AUC calculations
set.seed(2969)
imbal_train <- twoClassSim(5000,
intercept = -25,
linearVars = 20,
noiseVars = 10)
minorityClass = "Disease"
majorityClass = "Normal"
# 更改class信息,设置少数类,Disease为目标类,放在level第一位
imbal_train$Class = ifelse(imbal_train$Class == "Class1", majorityClass, minorityClass)
imbal_train$Class <- factor(imbal_train$Class, levels=c(minorityClass, majorityClass))
imbal_test <- twoClassSim(5000,
intercept = -25,
linearVars = 20,
noiseVars = 10)
imbal_test$Class = ifelse(imbal_test$Class == "Class1", majorityClass, minorityClass)
imbal_test$Class <- factor(imbal_test$Class, levels=c(minorityClass, majorityClass))
prop.table(table(imbal_train$Class))##
## Disease Normal
## 0.0204 0.9796prop.table(table(imbal_test$Class))##
## Disease Normal
## 0.0252 0.97483.5.1.1.1 构建原始GBM模型
这里应用另外一种集成学习算法 (GBM, Gradient Boosting Machine)进行模型构建。GBM也是效果很好的集成学习算法,可以处理变量的互作和非线性关系。机器学习中常用的GBDT、XGBoost和LightGBM算法(或工具)都是基于梯度提升机(GBM)的算法思想。
先构建一个原始模型,重复5次10-折交叉验证寻找最优的模型超参数,采用AUC作为评估标准。这些概念如果不熟悉翻一下往期推文。
# Set up control function for training
# 评估函数为twoClassSummary,评估指标为ROC曲线
ctrl <- trainControl(method = "repeatedcv",
number = 10,
repeats = 5,
summaryFunction = twoClassSummary,
classProbs = TRUE)
# Build a standard classifier using a gradient boosted machine
set.seed(5627)
orig_fit <- train(Class ~ .,
data = imbal_train,
method = "gbm",
verbose = FALSE,
metric = "ROC",
trControl = ctrl)
# Build custom AUC function to extract AUC
# from the caret model object
test_roc <- function(model, data) {
roc(data$Class,
predict(model, data, type = "prob")[, minorityClass])
}
orig_fit %>%
test_roc(data = imbal_test) %>%
auc()## Area under the curve: 0.9538AUC值为0.95,还是很不错的。从confusion matrix (预测结果采用默认阈值)来看,Class2的分类效果一般,准确率只有28.6%。不管是Class1还是Class2都倾向于预测为Class1,特异性低,这是因为样品不平衡导致的。假如Class2为疾病,我们通常更希望尽早发现疾病的存在。
predictions_train <- predict(orig_fit, newdata=imbal_test)
confusionMatrix(predictions_train, imbal_test$Class)## Confusion Matrix and Statistics
##
## Reference
## Prediction Disease Normal
## Disease 38 17
## Normal 88 4857
##
## Accuracy : 0.979
## 95% CI : (0.9746, 0.9828)
## No Information Rate : 0.9748
## P-Value [Acc > NIR] : 0.02954
##
## Kappa : 0.4109
##
## Mcnemar's Test P-Value : 8.415e-12
##
## Sensitivity : 0.3016
## Specificity : 0.9965
## Pos Pred Value : 0.6909
## Neg Pred Value : 0.9822
## Prevalence : 0.0252
## Detection Rate : 0.0076
## Detection Prevalence : 0.0110
## Balanced Accuracy : 0.6490
##
## 'Positive' Class : Disease
## confusionMatrix(predictions_train, imbal_test$Class, mode = "prec_recall")## Confusion Matrix and Statistics
##
## Reference
## Prediction Disease Normal
## Disease 38 17
## Normal 88 4857
##
## Accuracy : 0.979
## 95% CI : (0.9746, 0.9828)
## No Information Rate : 0.9748
## P-Value [Acc > NIR] : 0.02954
##
## Kappa : 0.4109
##
## Mcnemar's Test P-Value : 8.415e-12
##
## Precision : 0.6909
## Recall : 0.3016
## F1 : 0.4199
## Prevalence : 0.0252
## Detection Rate : 0.0076
## Detection Prevalence : 0.0110
## Balanced Accuracy : 0.6490
##
## 'Positive' Class : Disease
## 3.5.1.1.2 采用权重分配或抽样方式处理样品不平衡问题
这里应用的GBM模型自身有一个参数weights可以用于设置样品的权重;caret在trainControl函数中提供了sampling参数可以进行up-sample和down-sample,或其它任何算法的采样方式(这里用的是DMwR::SMOTE函数进行采样)。
# Create model weights (they sum to one)
# 给每一个观察一个权重
class1_weight = (1/table(imbal_train$Class)[[majorityClass]]) * 0.5
class2_weight = (1/table(imbal_train$Class)[[minorityClass]]) * 0.5
model_weights <- ifelse(imbal_train$Class == majorityClass,
class1_weight, class2_weight)
# Use the same seed to ensure same cross-validation splits
# 在处理多个模型时需要注意这一点
ctrl$seeds <- orig_fit$control$seeds
# Build weighted model
weighted_fit <- train(Class ~ .,
data = imbal_train,
method = "gbm",
verbose = FALSE,
weights = model_weights,
metric = "ROC",
trControl = ctrl)
# Build down-sampled model
ctrl$sampling <- "down"
down_fit <- train(Class ~ .,
data = imbal_train,
method = "gbm",
verbose = FALSE,
metric = "ROC",
trControl = ctrl)
# Build up-sampled model
ctrl$sampling <- "up"
up_fit <- train(Class ~ .,
data = imbal_train,
method = "gbm",
verbose = FALSE,
metric = "ROC",
trControl = ctrl)
# Build smote model
ctrl$sampling <- "smote"
smote_fit <- train(Class ~ .,
data = imbal_train,
method = "gbm",
verbose = FALSE,
metric = "ROC",
trControl = ctrl)计算下每个模型的AUC值
# Examine results for test set
model_list <- list(original = orig_fit,
weighted = weighted_fit,
down = down_fit,
up = up_fit,
SMOTE = smote_fit)
model_list_roc <- model_list %>%
map(test_roc, data = imbal_test)
model_list_roc %>%
map(auc)## $original
## Area under the curve: 0.9538
##
## $weighted
## Area under the curve: 0.9793
##
## $down
## Area under the curve: 0.9667
##
## $up
## Area under the curve: 0.9778
##
## $SMOTE
## Area under the curve: 0.9744样品加权模型获得的AUC值最高,其次是up-sample, SMOTE, down-sample,结果都比original有提高。
绘制下ROC曲线,查看下模型的具体效果展示。样品加权的模型优于其它所有模型,原始模型在假阳性率0-25%时效果差于其它模型。好的模型是在较低假阳性率时具有较高的真阳性率。
results_list_roc <- list(NA)
num_mod <- 1
for(the_roc in model_list_roc){
results_list_roc[[num_mod]] <-
data_frame(TPR = the_roc$sensitivities,
FPR = 1 - the_roc$specificities,
model = names(model_list)[num_mod])
num_mod <- num_mod + 1
}
results_df_roc <- bind_rows(results_list_roc)
results_df_roc$model <- factor(results_df_roc$model,
levels=c("original", "down","SMOTE","up","weighted"))
# Plot ROC curve for all 5 models
custom_col <- c("#000000", "#009E73", "#0072B2", "#D55E00", "#CC79A7")
ggplot(aes(x = FPR, y = TPR, group = model), data = results_df_roc) +
geom_line(aes(color = model), size = 1) +
scale_color_manual(values = custom_col) +
geom_abline(intercept = 0, slope = 1, color = "gray", size = 1) +
theme_bw(base_size = 18) + coord_fixed(1)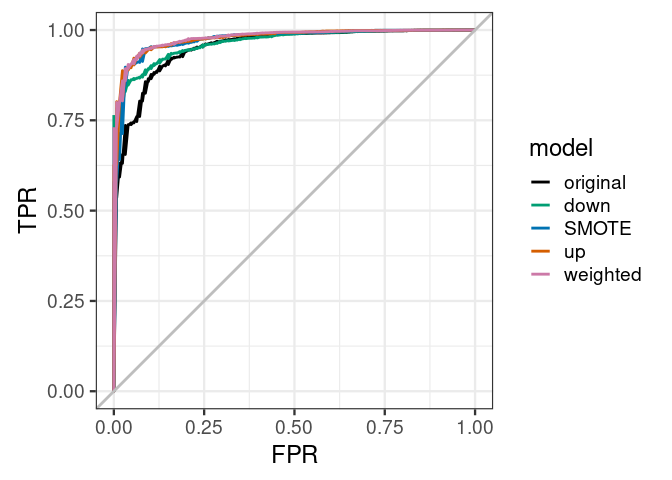
ggplot(aes(x = FPR, y = TPR, group = model), data = results_df_roc) +
geom_line(aes(color = model), size = 1) +
facet_wrap(vars(model)) +
scale_color_manual(values = custom_col) +
geom_abline(intercept = 0, slope = 1, color = "gray", size = 1) +
theme_bw(base_size = 18) + coord_fixed(1)
加权后的模型,总预测准确率降低了一点,但Disease的预测准确性升高了2.47倍,70.63%。
predictions_train <- predict(weighted_fit, newdata=imbal_test)
confusionMatrix(predictions_train, imbal_test$Class)## Confusion Matrix and Statistics
##
## Reference
## Prediction Disease Normal
## Disease 89 83
## Normal 37 4791
##
## Accuracy : 0.976
## 95% CI : (0.9714, 0.9801)
## No Information Rate : 0.9748
## P-Value [Acc > NIR] : 0.3137
##
## Kappa : 0.5853
##
## Mcnemar's Test P-Value : 3.992e-05
##
## Sensitivity : 0.7063
## Specificity : 0.9830
## Pos Pred Value : 0.5174
## Neg Pred Value : 0.9923
## Prevalence : 0.0252
## Detection Rate : 0.0178
## Detection Prevalence : 0.0344
## Balanced Accuracy : 0.8447
##
## 'Positive' Class : Disease
## confusionMatrix(predictions_train, imbal_test$Class, mode = "prec_recall")## Confusion Matrix and Statistics
##
## Reference
## Prediction Disease Normal
## Disease 89 83
## Normal 37 4791
##
## Accuracy : 0.976
## 95% CI : (0.9714, 0.9801)
## No Information Rate : 0.9748
## P-Value [Acc > NIR] : 0.3137
##
## Kappa : 0.5853
##
## Mcnemar's Test P-Value : 3.992e-05
##
## Precision : 0.5174
## Recall : 0.7063
## F1 : 0.5973
## Prevalence : 0.0252
## Detection Rate : 0.0178
## Detection Prevalence : 0.0344
## Balanced Accuracy : 0.8447
##
## 'Positive' Class : Disease
## 从这套测试数据来看,设置权重获得的模型效果是最好的。但这不是绝对的,应用于自己的数据时,需要都尝试一下,看看自己的数据更适合哪种方式。
3.5.1.1.3 ROC来评估不平衡数据集存在的问题
对于不平衡数据集,AUC值是分类器效果评估的常用标准。但如果在解释时不仔细,它也会有一些误导。以Davis and Goadrich (2006)中的模型为例。如 Fig (fig:rocprcompare)所示,左侧展示的是两个模型的ROC曲线,右侧展示的是precision-recall曲线 (PRC)。
Precision值和Recall值是既矛盾又统一的两个指标,为了提高Precision值,分类器需要尽量在“更有把握”时才把样本预测为正样本,但此时往往会因为过于保守而漏掉很多“没有把握”的正样本,导致Recall值降低。
RPC的横轴是召回率,纵轴是精准率。对于一个分类模型来说,其PRC线上的一个点代表着,在某一阈值下,模型将大于该阈值的结果判定为正样本,小于该阈值的结果判定为负样本,此时返回结果对应的召回率和精准率。整条PRC曲线是通过将阈值从高到低移动而生成的。 Fig (fig:rocprcompare) 是PRC曲线样例图,其中实线代表模型A的PRC曲线,虚线代表模型B的PRC曲线。原点附近代表当阈值最大时模型的精准率和召回率 (阈值越大,鉴定出的样品越真,能鉴定出的样品越少)。
模型1 (Curve 1)的AUC值为0.813, 模型2 (Curve 2)的AUC值为0.875, 从AUC值角度看模型2更优一点。但是右侧的precision-recall曲线却给出完全不同的结论。模型1 (precision-recall Curve 1)下的面积为0.513,模型2 (precision-recall Curve 2)下的面积为0.038。模型1在较低的假阳性率(FPR<0.2)时有较高的真阳性率。
knitr::include_graphics("images/roc_pr_compare.png")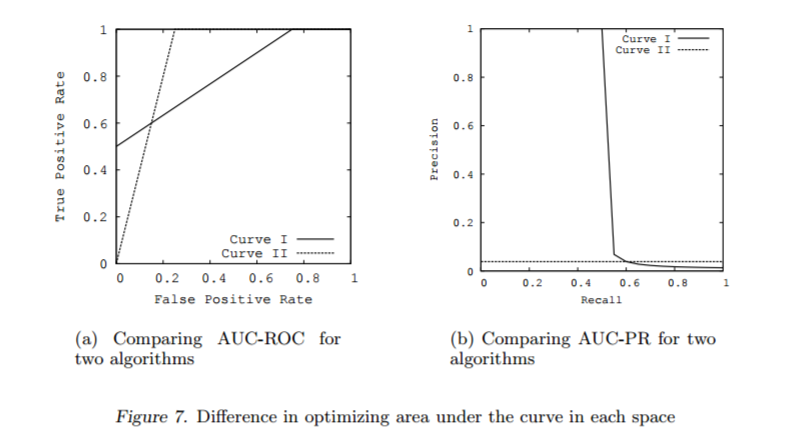
Figure 3.5: area under the ROC curve (AUC) and area under the precision-recall curve (AUPRC).
我们再看另一个关于ROC曲线误导性的例子 Fawcett (2005). 这里有两套数据集:一套为平衡数据集(两类分组为1:1关系),一套为非平衡数据集(两类分组为10:1关系)。每套数据集分别构建2个模型并绘制ROC曲线,从Fig (fig:rocprbalanceimbalance) a,c 可以看出,数据集是否平衡对ROC曲线的影响很小。只是在两个模型之间有一些差别,实线代表的模型在假阳性率较低时 (FPR<0.1)真阳性率低于虚线代表的模型。但precision-recall curve (PRC)曲线却差别很大。对于平衡数据集,两个模型的召回率 (recall)和精准率precision都比较好。对于非平衡数据集,虚线代表的分类模型在较低的召回率时就有较高的精准率。
knitr::include_graphics("images/roc_pr_balance_imbalance.png")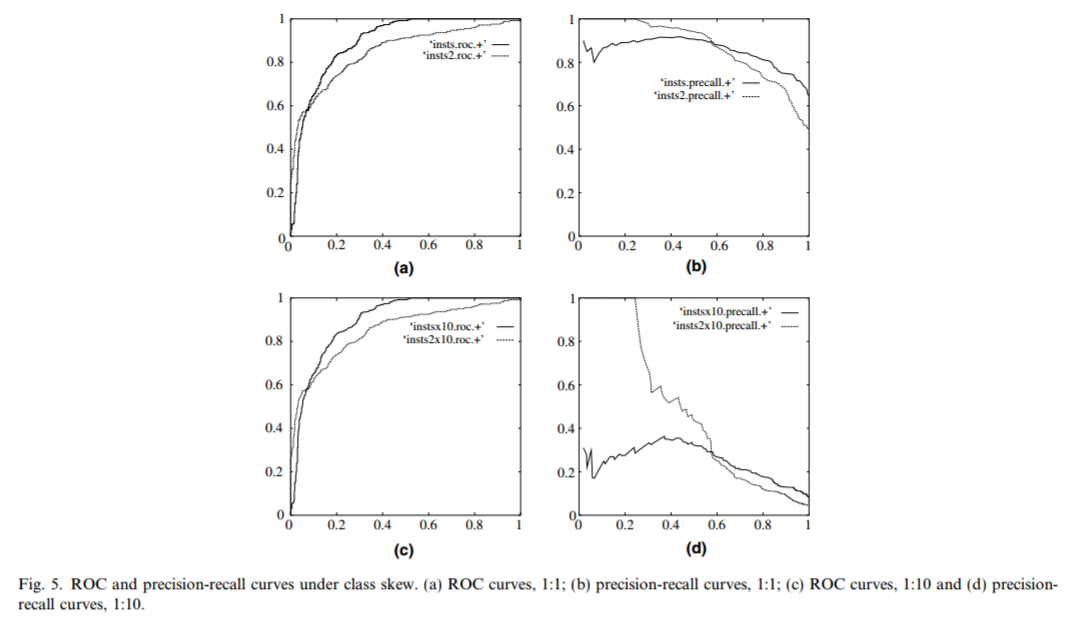
因此,Saito and Rehmsmeier (2015)推荐在处理非平衡数据集时使用PRC曲线,它所反映的信息比ROC曲线更明确。
我们对前面5个模型计算下AUPRC,与AUC结果基本吻合,up效果最好,其次是weighted, smote, down和original。值得差距稍微拉大了一些。
library("PRROC")
calc_auprc <- function(model, data){
index_class2 <- data$Class == minorityClass
index_class1 <- data$Class == majorityClass
predictions <- predict(model, data, type = "prob")
pr.curve(predictions[[minorityClass]][index_class2],
predictions[[minorityClass]][index_class1],
curve = TRUE)
}
# Get results for all 5 models
model_list_pr <- model_list %>%
map(calc_auprc, data = imbal_test)
model_list_pr %>%
map(function(the_mod) the_mod$auc.integral)## $original
## [1] 0.5155589
##
## $weighted
## [1] 0.640687
##
## $down
## [1] 0.5302778
##
## $up
## [1] 0.6461067
##
## $SMOTE
## [1] 0.6162899我们绘制PRC曲线观察各个模型的分类效果。基于选定的分类阈值,up sampling和weighting有着最好的精准率和召回率 (单个分组的准确率)。而原始分类器则效果最差。假如加权分类器在召回率 (recall)为75%时,精准率可以达到50% (下面曲线中略低于50%),则F1得分为0.6。原始分类器在召回率为75%时,精准率为25% (下面曲线略高于25%),则F1得分为0.38。也就是说,当构建好了这两个分类器,并设置一个分类阈值 (不同模型的阈值不同)后,都可以在样品少的分组中获得75%的召回率。但是对于加权模型,有50%的预测为属于样品少的分组的样品是预测对的。而对于原始模型,只有25%预测为属于样品少的分组的样品是预测对的。
# Plot the AUPRC curve for all 5 models
results_list_pr <- list(NA)
num_mod <- 1
for(the_pr in model_list_pr){
results_list_pr[[num_mod]] <-
data_frame(recall = the_pr$curve[, 1],
precision = the_pr$curve[, 2],
model = names(model_list_pr)[num_mod])
num_mod <- num_mod + 1
}
results_df_pr <- bind_rows(results_list_pr)
results_df_pr$model <- factor(results_df_pr$model,
levels=c("original", "down","SMOTE","up","weighted"))
# Plot ROC curve for all 5 models
custom_col <- c("#000000", "#009E73", "#0072B2", "#D55E00", "#CC79A7")
ggplot(aes(x = recall, y = precision, group = model), data = results_df_pr) +
geom_line(aes(color = model), size = 1) +
scale_color_manual(values = custom_col) +
geom_abline(intercept =
sum(imbal_test$Class == minorityClass)/nrow(imbal_test),
slope = 0, color = "gray", size = 1) +
theme_bw(base_size = 18) + coord_fixed(1)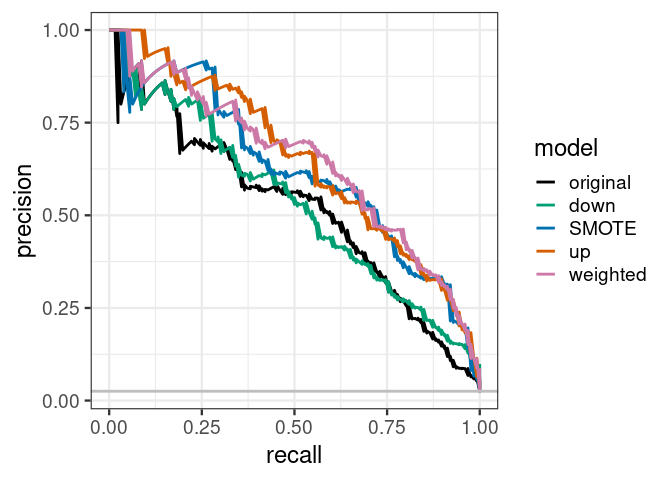
基于AUPRC进行调参,修改参数summaryFunction = prSummary和metric = "AUC"。参考https://topepo.github.io/caret/measuring-performance.html。
# Set up control function for training
ctrlprSummary <- trainControl(method = "repeatedcv",
number = 10,
repeats = 5,
summaryFunction = prSummary,
classProbs = TRUE)
# Build a standard classifier using a gradient boosted machine
set.seed(5627)
orig_fit2 <- train(Class ~ .,
data = imbal_train,
method = "gbm",
verbose = FALSE,
metric = "AUC",
trControl = ctrlprSummary)
# Use the same seed to ensure same cross-validation splits
ctrlprSummary$seeds <- orig_fit$control$seeds
# Build weighted model
weighted_fit2 <- train(Class ~ .,
data = imbal_train,
method = "gbm",
verbose = FALSE,
weights = model_weights,
metric = "AUC",
trControl = ctrlprSummary)
# Build down-sampled model
ctrlprSummary$sampling <- "down"
down_fit2 <- train(Class ~ .,
data = imbal_train,
method = "gbm",
verbose = FALSE,
metric = "AUC",
trControl = ctrlprSummary)
# Build up-sampled model
ctrlprSummary$sampling <- "up"
up_fit2 <- train(Class ~ .,
data = imbal_train,
method = "gbm",
verbose = FALSE,
metric = "AUC",
trControl = ctrlprSummary)
# Build smote model
ctrlprSummary$sampling <- "smote"
smote_fit2 <- train(Class ~ .,
data = imbal_train,
method = "gbm",
verbose = FALSE,
metric = "AUC",
trControl = ctrlprSummary)
model_list2 <- list(original = orig_fit2,
weighted = weighted_fit2,
down = down_fit2,
up = up_fit2,
SMOTE = smote_fit2)评估下基于prSummary调参后模型的性能,SMOTE处理后的模型效果有提升,其它模型相差不大。
model_list_pr2 <- model_list2 %>%
map(calc_auprc, data = imbal_test)
model_list_pr2 %>%
map(function(the_mod) the_mod$auc.integral)## $original
## [1] 0.5155589
##
## $weighted
## [1] 0.640687
##
## $down
## [1] 0.5302778
##
## $up
## [1] 0.6461067
##
## $SMOTE
## [1] 0.6341753# Plot the AUPRC curve for all 5 models
results_list_pr <- list(NA)
num_mod <- 1
for(the_pr in model_list_pr2){
results_list_pr[[num_mod]] <-
data_frame(recall = the_pr$curve[, 1],
precision = the_pr$curve[, 2],
model = names(model_list_pr)[num_mod])
num_mod <- num_mod + 1
}
results_df_pr <- bind_rows(results_list_pr)
results_df_pr$model <- factor(results_df_pr$model,
levels=c("original", "down","SMOTE","up","weighted"))
# Plot ROC curve for all 5 models
custom_col <- c("#000000", "#009E73", "#0072B2", "#D55E00", "#CC79A7")
ggplot(aes(x = recall, y = precision, group = model), data = results_df_pr) +
geom_line(aes(color = model), size = 1) +
scale_color_manual(values = custom_col) +
geom_abline(intercept =
sum(imbal_test$Class == minorityClass)/nrow(imbal_test),
slope = 0, color = "gray", size = 1) +
theme_bw(base_size = 18) + coord_fixed(1)
PRC和AUPRC是处理非平衡数据集的有效衡量方式。基于AUC指标来看,权重和重采样技术只带来了微弱的性能提升。但是这个改善更多体现在可以在较低假阳性率基础上获得较高真阳性率,模型的性能更均匀提升。在处理非平衡样本学习问题时,除了尝试调整权重和重采样之外,也不能完全依赖AUC值,而是依靠PRC曲线联合判断,以期获得更好的效果。
3.5.1.2 样品组设置不同的权重
样品少的分组在分类决策时对决策树分支的Gini impurity贡献小,为了规避这一影响,我们需要对误分类样品少的分组时给予更多的罚分 (ost sensitive learning: assigning a high cost to mis-classification of the minority class, and trying to minimize the overall cost)。
计算每个样品的权重 (样品所占比例的倒数)
group_count <- table(metadata[[group]])
group_freq <- group_count / sum(group_count)
group_weight <- 1/group_freq
group_weight <- data.frame(Name=names(group_weight), Weight=as.vector(group_weight))
colnames(group_weight) <- c(group,"Case_weight")
group_weight## class Case_weight
## 1 DLBCL 1.327586
## 2 FL 4.052632library(caret)
caretRun <- function (ml_method, train_data, rda_dir="rda/") {
dir.create(rda_dir, showWarnings = F, recursive = T)
mtry <- generateTestVariableSet(ncol(train_data))
# Create model with default parameters
trControl <- trainControl(method = "repeatedcv",
number = 10,
repeats = 5)
# train model
if (file.exists('rda/rangerBalanceCaseWeight.rda')) {
rangerBalanceCaseWeigh <- readRDS("rda/rangerBalanceCaseWeigh.rda")
} else {
# 设置随机数种子,使得结果可重复
seed <- 1
set.seed(seed)
# 根据经验或感觉设置一些待查询的参数和参数值
tuneGrid <- expand.grid(mtry = boruta_mtry)
borutaConfirmed_rf_default <-
train(
x = boruta_train_data,
y = train_data_group,
method = "rf",
tuneGrid = tuneGrid,
#
metric = "Accuracy",
#metric='Kappa'
trControl = trControl
)
saveRDS(borutaConfirmed_rf_default,
"rda/borutaConfirmed_rf_default.rda")
}
}
print(borutaConfirmed_rf_default)mtry <- generateTestVariableSet(ncol(train_data))
library(caret)
# Create model with default parameters
trControl <- trainControl(method="repeatedcv", number=10, repeats=5)
# train model
if(file.exists('rda/rangerBalanceCaseWeight.rda')){
rangerBalanceCaseWeigh <- readRDS("rda/rangerBalanceCaseWeigh.rda")
} else {
# 设置随机数种子,使得结果可重复
seed <- 1
set.seed(seed)
# 根据经验或感觉设置一些待查询的参数和参数值
tuneGrid <- expand.grid(mtry=boruta_mtry)
borutaConfirmed_rf_default <- train(x=boruta_train_data, y=train_data_group, method="rf",
tuneGrid = tuneGrid, #
metric="Accuracy", #metric='Kappa'
trControl=trControl)
saveRDS(borutaConfirmed_rf_default, "rda/borutaConfirmed_rf_default.rda")
}
print(borutaConfirmed_rf_default)# 获得模型结果评估矩阵(`confusion matrix`)
predictions_train <- predict(borutaConfirmed_rf_default_finalmodel, newdata=train_data)
confusionMatrix(predictions_train, train_data_group)library(ranger)
model <- ranger(Y~., data, case.weights=metadata$Case_weight)
print(model)3.5.1.3 数据抽样
a sampling technique: Either down-sampling the majority class or over-sampling the minority class,or both.
3.5.2 填补伪数据
table(metadata[[group]])平衡样本
sampszize=rep(length(minorityClass),2)3.5.3 读入数据
这里直接读入前面拆分好的训练集、测试集数据(只保留了Boruta评估后对分类有显著意义的变量)
train_boruta_data <- sp_readTable("data/DLBCL.train.boruta.txt", row.names=1)
train_boruta_group <- as.factor(sp_readTable("data/DLBCL.train.group.txt", row.names=1)[['class']])
test_boruta_data <- sp_readTable("data/DLBCL.test.boruta.txt", row.names=1)
test_boruta_group <- as.factor(sp_readTable("data/DLBCL.test.group.txt", row.names=1)[['class']])3.5.4 直接使用randomForest包进行分析和测试
library(randomForest)
# 查看参数是个好习惯
# 有了前面的基础概述,再看每个参数的含义就明确了很多
# 也知道该怎么调了
# 每个人要解决的问题不同,通常不是别人用什么参数,自己就跟着用什么参数
# 尤其是到下游分析时
# ?randomForest
# 查看源码
# randomForest:::randomForest.default加载包之后,直接分析一下,看到结果再调参。
# 设置随机数种子,具体含义见 https://mp.weixin.qq.com/s/6plxo-E8qCdlzCgN8E90zg
set.seed(304)
# 直接使用默认参数
rf <- randomForest(train_boruta_data, train_boruta_group)rftable(train_boruta_group)rf <- randomForest(train_boruta_data, train_boruta_group, ntree=4000, samplesize=c(44,44), strata=train_boruta_group)
rfgroup_count <- table(train_boruta_group)
group_freq <- group_count / sum(group_count)
group_weight <- 1/group_freq
group_weight <- data.frame(Name=names(group_weight), Weight=as.vector(group_weight))
colnames(group_weight) <- c(group,"Case_weight")
group_weightlibrary(ranger)
model <- ranger(Y~., data, case.weights=metadata$Case_weight)
print(model)