5 特征选择

5.1 特征选择概述

高维数据包括的检测变量越来越多，如基因表达数据中检测到的基因数目、扩增子测序中的OTU数目等。在训练模型时通常需要先对数据去冗余，提取一些关键变量。这不只可以加速模型的构建还可以降低模型的复杂度，使其更易于解释 (而不只是一个预测黑盒子)。同时也有助于提高模型的性能（或在不损失太多模型性能的基础上获得更简单的模型），降低过拟合问题的出现。

主成分分析、奇异值分解是常用的降维方式。如PCA通过把原始变量进行线性组合获得主成分就是一个特征选择的过程。在使用tSNE算法进行单细胞聚类时使用的就是核心的主成分。但PCA等未考虑原始特征值与其所属分类或响应值的关系。因此并不适用于所有的情况。

有一些算法如随机森林等在构建模型时可以自己选择有最合适的分类或预测能力的特征集合。前面提到，基于随机置换的变量的整体重要性得分(ACS)是评估变量重要性的一个比较可靠的方式。但这种方式获得的ACS Z-score只能用于排序确定哪些变量更重要，但不能根据统计显著性获得所有重要的变量。因此如果我们的目的还希望鉴定出哪些特征对分类或预测有贡献时，还需要借助其他的方式。

特征递归消除(RFE, recursive feature elimination)是一个常用的方法；它基于模型预测性能评估指标如准确性等选择一个性能较佳的最小集合的特征变量。它首先应用所有的特征变量构建模型，然后移除对模型最不重要的一定比例的变量再次构建模型；持续迭代直至获得准确性最高的模型。

在后续应用预测模型时，只需要使用数目比较少的变量，这样的好处是便于新样品的变量检测。但在临床应用时，不同的数据集包含的变量可能相差较大，共有的变量较少，但却可以获得相似的预测性能。其中一个主要原因是组学数据中，很多变量之间是相关性比较强的。因此不同的变量集合可能会获得同样的预测性能。而在构建模型时保留这些相关的冗余变量可以获得更稳定、准确的预测结果，同时对病理机制也能提供更全面的解释。

其它变量选择方法不去除冗余变量，而是通过估计不相干变量的重要性值的分布，选择具有显著更高重要性值的变量作为预测变量。这些方法越来越受欢迎。包括permutation (Perm)和它的参数化版本Altmann,Boruta, r2VIM (recurrent relative variable importance)和Vita。在2019年的一篇基于组学数据的评估文章中得出结论：Boruta和Vita算法的稳定性最好，适合分析高维数据。Vita的计算速度比Boruta快很多更适合大数据集，但只有Boruta可用于低维数据。 (https://doi.org/10.1093/bib/bbx124)

5.1.1 特征选择方法比较

Abbreviation	Name	Goal	Approach	R package	Citationsa
Altmann	Altmann	All relevant variables	Permutation of outcome; parametric P-value	R code on first author’s Web site (http://www.altmann.eu/documents/PIMP.R) Implemented in ranger package (https://cran.r-project.org/web/packages/ranger/index.html) and vita package (https://cran.r-project.org/web/packages/vita/index.html)	511
Boruta	Boruta	All relevant variables	Importance significantly larger than those of shadow variables	Boruta (https://cran.r-project.org/web/packages/Boruta/index.html)	1271
Perm	Permutation	All relevant variables	Permutations of outcome; nonparametric P-value	No specific implementation for RF	–
r2VIM	Recurrent relative variable importance	All relevant variables	Relative importance based on minimal observed importance; several runs of RF	r2VIM (http://research.nhgri.nih.gov/software/r2VIM)	35
RFE	Recursive feature elimination	Minimal set	RF with smallest error based on iterative removal of least important variables	varSelRF (https://cran.r-project.org/web/packages/varSelRF/index.html)	2668
Vita	Vita	All relevant variables	P-values based on empirical null distribution based on non-positive importance scores calculated using hold-out approach	Vita (https://cran.r-project.org/web/packages/vita/index.html) Implemented in ranger package (https://cran.r-project.org/web/packages/ranger/index.html)	82

5.2 Boruta算法

5.2.1 Boruta算法概述

Boruta得名于斯拉夫神话中的树神，可以识别所有对分类或回归有显著贡献的变量。其核心思想是统计比较数据中真实存在的特征变量与随机加入的变量（也称为影子变量）的重要性。

1. 初次建模时，把原始变量拷贝一份作为影子变量。
2. 原始变量的值随机化后作为对应影子变量的值 (随机化就是打乱原始变量值的顺序)。
3. 使用随机森林建模并计算每个变量的重要性得分。
4. 对于每一个真实特征变量，统计检验其与所有影子变量的重要性最大值的差别。重要性显著高于影子变量的真实特征变量定义为重要。重要性显著低于影子变量的真实特征变量定义为不重要。
5. 所有不重要的变量和影子变量移除。
6. 基于新变量构成的数据集再次重复刚才的建模和选择过程，直到所有变量都被分类为重要或不重要，或达到预先设置的迭代次数。

Figure 5.1: https://en.wikipedia.org/wiki/Devil_Boruta

其优点是：

1. 同时适用于分类问题和回归问题
2. 考虑多个变量的关系信息
3. 改善了常用于变量选择的随机森林变量重要性计算方式
4. 会输出所有与模型性能相关的变量而不是只返回一个最小变量集合
5. 可以处理变量的互作
6. 可以规避随机森林自身计算变量重要性的随机波动性问题和不能计算显著性的问题

5.2.2 Boruta算法实战

# install.packages("Boruta")
library(Boruta)

set.seed(1)
if(file.exists('rda/boruta300.rda')){
   boruta <- readRDS("rda/boruta300.rda")
} else {
  boruta <- Boruta(x=train_data, y=train_data_group, pValue=0.01, mcAdj=T, 
       maxRuns=300)
  saveRDS(boruta, "rda/boruta300.rda")
}

boruta

## Boruta performed 299 iterations in 1.28454 mins.
##  54 attributes confirmed important: AC002073_cds1_at, D13633_at,
## D31887_at, D55716_at, D78134_at and 49 more;
##  6980 attributes confirmed unimportant: A28102, AB000114_at,
## AB000115_at, AB000220_at, AB000381_s_at and 6975 more;
##  36 tentative attributes left: D31886_at, D43950_at, D79997_at,
## HG2279.HT2375_at, HG417.HT417_s_at and 31 more;

速度还是可以的 (1-2 分钟)（尤其是跟后面要介绍的 RFE 的速度比起来）

boruta$timeTaken

## Time difference of 1.28454 mins

查看下变量重要性鉴定结果（实际上面的输出中也已经有体现了），54个重要的变量，36个可能重要的变量 (tentative variable, 重要性得分与最好的影子变量得分无统计差异)，6,980个不重要的变量。

table(boruta$finalDecision)

## 
## Tentative Confirmed  Rejected 
##        36        54      6980

boruta$finalDecision[boruta$finalDecision=="Confirmed"]

## AC002073_cds1_at        D13633_at        D31887_at        D55716_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
##        D78134_at        D82348_at        D87119_at HG2874.HT3018_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
## HG4074.HT4344_at HG4258.HT4528_at        J02645_at        J03909_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
##        K02268_at   L17131_rna1_at        L27071_at        L42324_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
##        M10901_at        M57710_at        M60830_at        M63138_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
##        M63835_at        U14518_at        U23143_at        U28386_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
##        U37352_at        U38896_at        U56102_at        U59309_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
##        U63743_at        U68030_at        X01060_at        X02152_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
##        X14850_at        X16983_at        X17620_at        X56494_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
##        X62078_at        X67155_at        X67951_at        X69433_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
##        Z11793_at        Z21966_at        Z35227_at        Z96810_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
##        U16307_at HG3928.HT4198_at      V00594_s_at      X03689_s_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
##      M14328_s_at      X91911_s_at      X12530_s_at      X81836_s_at 
##        Confirmed        Confirmed        Confirmed        Confirmed 
## HG1980.HT2023_at      M94880_f_at 
##        Confirmed        Confirmed 
## Levels: Tentative Confirmed Rejected

绘制Boruta算法运行过程中各个变量的重要性得分的变化 （绿色是重要的变量，红色是不重要的变量，蓝色是影子变量，黄色是Tentative变量）。

这个图也可以用来查看是否有必要增加迭代的次数以便再次确认Tentative变量中是否有一部分为有意义的特征变量。从下图来看，黄色变量部分随着迭代还是有部分可能高于最高值，可以继续尝试增加迭代次数。

Boruta::plotImpHistory(boruta)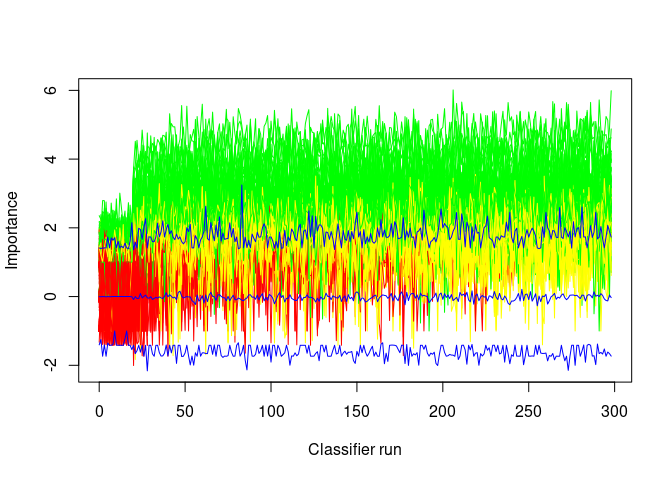

绘制鉴定出的变量的重要性。变量少了可以用默认绘图，变量多时绘制的图看不清，需要自己整理数据绘图。

# ?plot.Boruta
# plot(boruta)

定义一个函数提取每个变量对应的重要性值。

library(dplyr)
boruta.imp <- function(x){
  imp <- reshape2::melt(x$ImpHistory, na.rm=T)[,-1]
  colnames(imp) <- c("Variable","Importance")
  imp <- imp[is.finite(imp$Importance),]
  
  variableGrp <- data.frame(Variable=names(x$finalDecision), 
                            finalDecision=x$finalDecision)
  
  showGrp <- data.frame(Variable=c("shadowMax", "shadowMean", "shadowMin"),
                        finalDecision=c("shadowMax", "shadowMean", "shadowMin"))
  
  variableGrp <- rbind(variableGrp, showGrp)
  
  boruta.variable.imp <- merge(imp, variableGrp, all.x=T)
  
  sortedVariable <- boruta.variable.imp %>% group_by(Variable) %>% 
    summarise(median=median(Importance)) %>% arrange(median)
  sortedVariable <- as.vector(sortedVariable$Variable)
  
  
  boruta.variable.imp$Variable <- factor(boruta.variable.imp$Variable, levels=sortedVariable)
  
  invisible(boruta.variable.imp)
}

boruta.variable.imp <- boruta.imp(boruta)

head(boruta.variable.imp)

##   Variable Importance finalDecision
## 1   A28102          0      Rejected
## 2   A28102          0      Rejected
## 3   A28102          0      Rejected
## 4   A28102          0      Rejected
## 5   A28102          0      Rejected
## 6   A28102          0      Rejected

只绘制Confirmed变量。

library(ImageGP)

sp_boxplot(boruta.variable.imp, melted=T, xvariable = "Variable", yvariable = "Importance",
           legend_variable = "finalDecision", legend_variable_order = c("shadowMax", "shadowMean", "shadowMin", "Confirmed"),
           xtics_angle = 90)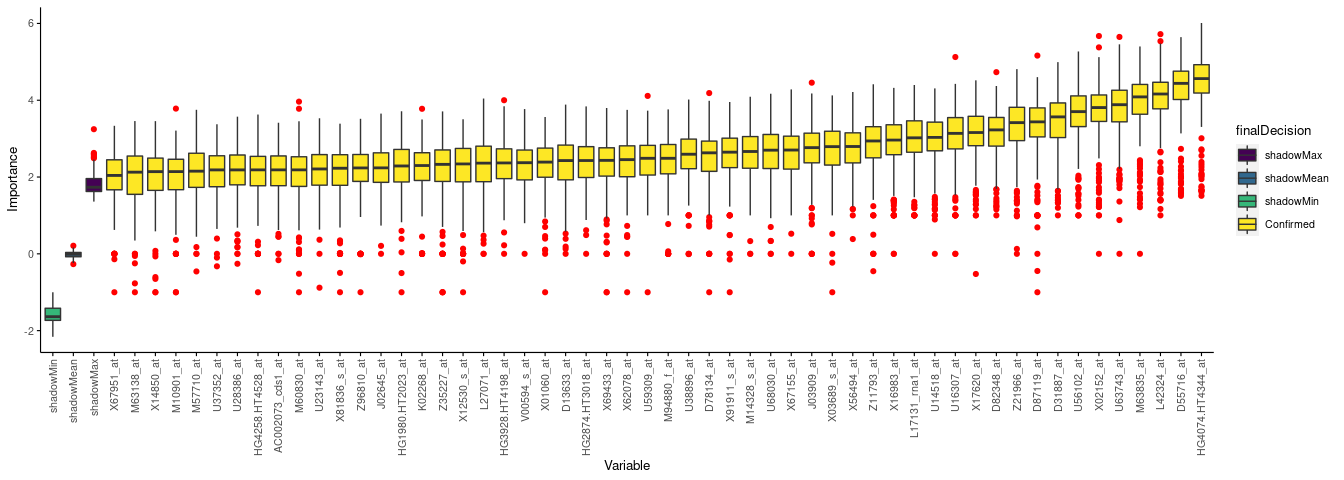

提取重要的变量 (可能重要的变量可提取可不提取)

boruta.finalVars <- data.frame(Item=getSelectedAttributes(boruta, withTentative = F), Type="Boruta")
boruta.finalVarsWithTentative <- data.frame(Item=getSelectedAttributes(boruta, withTentative = T), Type="Boruta_with_tentative")

也可以使用TentativeRoughFix函数进一步计算。这一步的计算比较粗糙，根据重要性的值高低判断Tentative类型的变量是否要为Confirmed或Rejected。

Tentative.boruta <- TentativeRoughFix(boruta)

看下这些变量的值的分布

caret::featurePlot(train_data[,boruta.finalVars$Item], train_data_group, plot="box")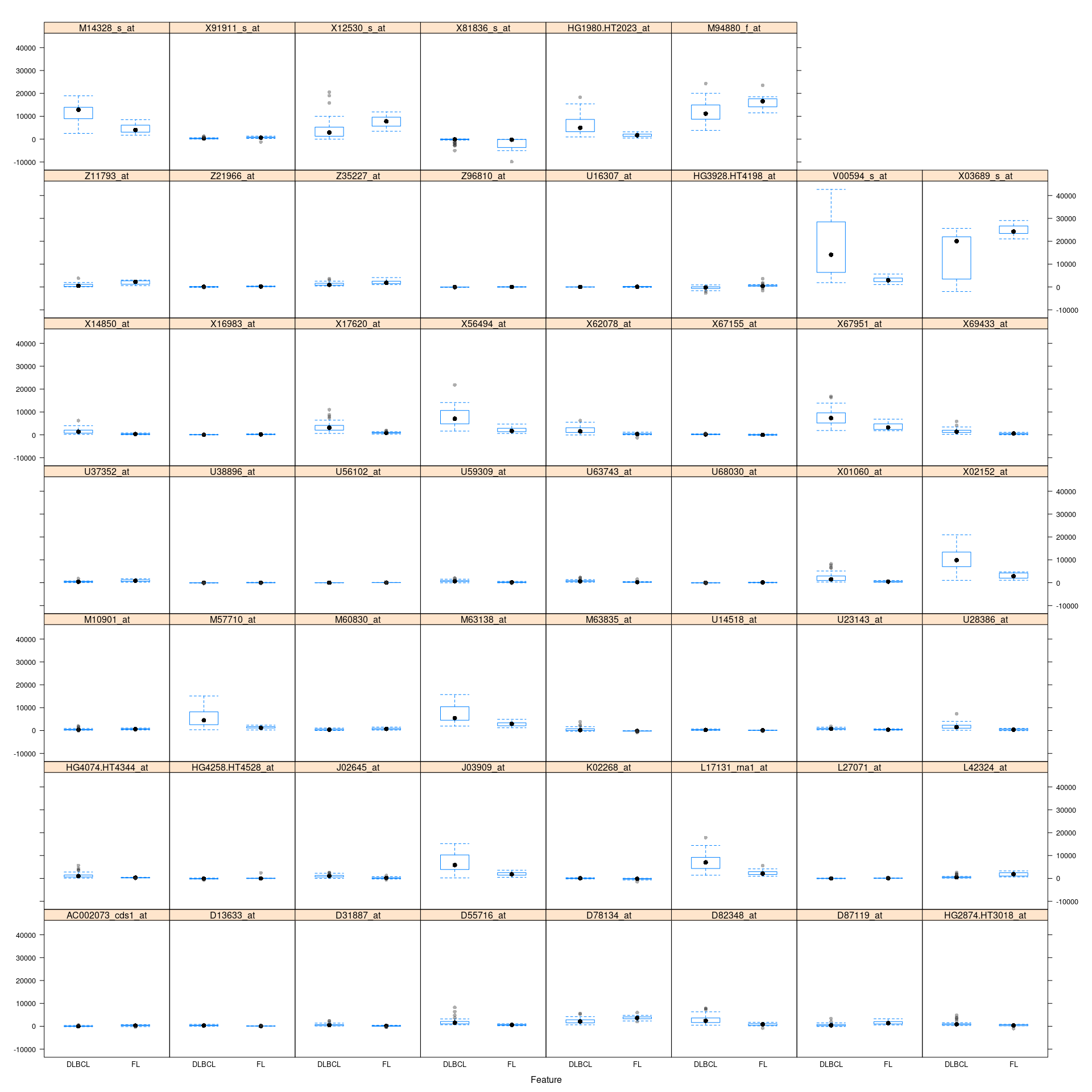

5.2.3 Boruta 选择的变量拟合模型

5.2.3.1 Boruta 选择的所有重要的变量拟合模型

定义一个函数生成一些列用来测试的mtry (一系列不大于总变量数的数值)。

generateTestVariableSet <- function(num_toal_variable){
  max_power <- ceiling(log10(num_toal_variable))
  tmp_subset <- unique(unlist(sapply(1:max_power, function(x) (1:10)^x, simplify = F)))
  sort(tmp_subset[tmp_subset<num_toal_variable])
}

选择关键特征变量相关的数据

# withTentative=F: 不包含tentative变量
boruta.confirmed <- getSelectedAttributes(boruta, withTentative = F)

# 提取训练集的特征变量子集
boruta_train_data <- train_data[, boruta.confirmed, drop=F]
boruta_mtry <- generateTestVariableSet(length(boruta.confirmed))

使用 Caret 进行调参和建模

library(caret)
# Create model with default parameters
trControl <- trainControl(method="repeatedcv", number=10, repeats=5)

# train model
if(file.exists('rda/borutaConfirmed_rf_default.rda')){
   borutaConfirmed_rf_default <- readRDS("rda/borutaConfirmed_rf_default.rda")
} else {
  # 设置随机数种子，使得结果可重复
  seed <- 1
  set.seed(seed)
  # 根据经验或感觉设置一些待查询的参数和参数值
  tuneGrid <- expand.grid(mtry=boruta_mtry)
  
  borutaConfirmed_rf_default <- train(x=boruta_train_data, y=train_data_group, method="rf", 
                     tuneGrid = tuneGrid, # 
                     metric="Accuracy", #metric='Kappa'
                     trControl=trControl)
  saveRDS(borutaConfirmed_rf_default, "rda/borutaConfirmed_rf_default.rda")
}
print(borutaConfirmed_rf_default)

## Random Forest 
## 
## 59 samples
## 56 predictors
##  2 classes: 'DLBCL', 'FL' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 5 times) 
## Summary of sample sizes: 53, 54, 53, 54, 53, 52, ... 
## Resampling results across tuning parameters:
## 
##   mtry  Accuracy   Kappa    
##    1    0.9862857  0.9565868
##    2    0.9632381  0.8898836
##    3    0.9519048  0.8413122
##    4    0.9519048  0.8413122
##    5    0.9519048  0.8413122
##    6    0.9519048  0.8413122
##    7    0.9552381  0.8498836
##    8    0.9519048  0.8413122
##    9    0.9547619  0.8473992
##   10    0.9519048  0.8413122
##   16    0.9479048  0.8361174
##   25    0.9519048  0.8413122
##   36    0.9450476  0.8282044
##   49    0.9421905  0.8199691
## 
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 1.

提取最终选择的模型，并绘制 ROC 曲线。

# Just to clarify this later point a bit further: predict(xx$finalModel, testData) and predict(xx, testData) will be different if one sets the preProcess option when using train. 
# On the other hand, when using the finalModel directly it is equivalent using the predict function from the model fitted (predict.randomForest here) instead of predict.train; no pre-proessing takes place. 
# borutaConfirmed_rf_default_finalmodel <- borutaConfirmed_rf_default$finalModel

采用训练数据集评估构建的模型，Accuracy=1; Kappa=1，非常完美。

模型的预测显著性P-Value [Acc > NIR] : 3.044e-08。其中NIR是No Information Rate，其计算方式为数据集中最大的类包含的数据占总数据集的比例。如某套数据中，分组A有80个样品，分组B有20个样品，我们只要猜A，正确率就会有80%，这就是NIR。如果基于这套数据构建的模型准确率也是80%，那么这个看上去准确率较高的模型也没有意义。confusionMatrix使用binom.test函数检验模型的准确性Accuracy是否显著优于NIR，若P-value<0.05，则表示模型预测准确率显著高于随便猜测。

# 获得模型结果评估矩阵(`confusion matrix`)

predictions_train <- predict(borutaConfirmed_rf_default, newdata=train_data)
confusionMatrix(predictions_train, train_data_group)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction DLBCL FL
##      DLBCL    44  0
##      FL        0 15
##                                      
##                Accuracy : 1          
##                  95% CI : (0.9394, 1)
##     No Information Rate : 0.7458     
##     P-Value [Acc > NIR] : 3.044e-08  
##                                      
##                   Kappa : 1          
##                                      
##  Mcnemar's Test P-Value : NA         
##                                      
##             Sensitivity : 1.0000     
##             Specificity : 1.0000     
##          Pos Pred Value : 1.0000     
##          Neg Pred Value : 1.0000     
##              Prevalence : 0.7458     
##          Detection Rate : 0.7458     
##    Detection Prevalence : 0.7458     
##       Balanced Accuracy : 1.0000     
##                                      
##        'Positive' Class : DLBCL      
## 

绘制ROC曲线，计算模型整体的AUC值，并选择最佳模型。

# 绘制ROC曲线

prediction_prob <- predict(borutaConfirmed_rf_default, newdata=test_data, type="prob")
library(pROC)
roc_curve <- roc(test_data_group, prediction_prob[,1])
#roc <- roc(test_data_group, factor(predictions, ordered=T))

roc_curve

## 
## Call:
## roc.default(response = test_data_group, predictor = prediction_prob[,     1])
## 
## Data: prediction_prob[, 1] in 14 controls (test_data_group DLBCL) > 4 cases (test_data_group FL).
## Area under the curve: 0.9821

选择最佳阈值 (https://stats.stackexchange.com/questions/312780/why-is-accuracy-not-the-best-measure-for-assessing-classification-models)

• youden: \(max(sensitivities + r \times specificities)\)
• closest.topleft: \(min((1 - sensitivities)^2 + r \times (1- specificities)^2)\)

r是加权系数，默认是1，其计算方式为\(r = (1 - prevalence) / (cost * prevalence)\).

best.weights控制加权方式：(cost, prevalence)默认是(1, 0.5)，据此算出的r为1。

• cost: 假阴性率占假阳性率的比例，容忍更高的假阳性率还是假阴性率

• prevalence: 关注的类中的个体所占的比例 (n.cases/(n.controls+n.cases)).

best_thresh <- data.frame(coords(roc=roc_curve, x = "best", input="threshold", 
                                 transpose = F, best.method = "youden"))
best_thresh

##   threshold specificity sensitivity
## 1     0.736   0.9285714           1

准备数据绘制ROC曲线

library(ggrepel)
ROC_data <- data.frame(FPR = 1- roc_curve$specificities, TPR=roc_curve$sensitivities)
ROC_data <- ROC_data[with(ROC_data, order(FPR,TPR)),]

best_thresh$best <- apply(best_thresh, 1, function (x) 
  paste0('threshold: ', x[1], ' (', round(1-x[2],3), ", ", round(x[3],3), ")"))

p <- ggplot(data=ROC_data, mapping=aes(x=FPR, y=TPR)) +
  geom_step(color="red", size=1, direction = "vh") +
  geom_segment(aes(x=0, xend=1, y=0, yend=1))  + theme_classic() + 
  xlab("False positive rate") + 
  ylab("True positive rate") + coord_fixed(1) + xlim(0,1) + ylim(0,1) +
  annotate('text', x=0.5, y=0.25, label=paste('AUC=', round(roc$auc,2))) +
  geom_point(data=best_thresh, mapping=aes(x=1-specificity, y=sensitivity), color='blue', size=2) + 
  geom_text_repel(data=best_thresh, mapping=aes(x=1.05-specificity, y=sensitivity ,label=best))
p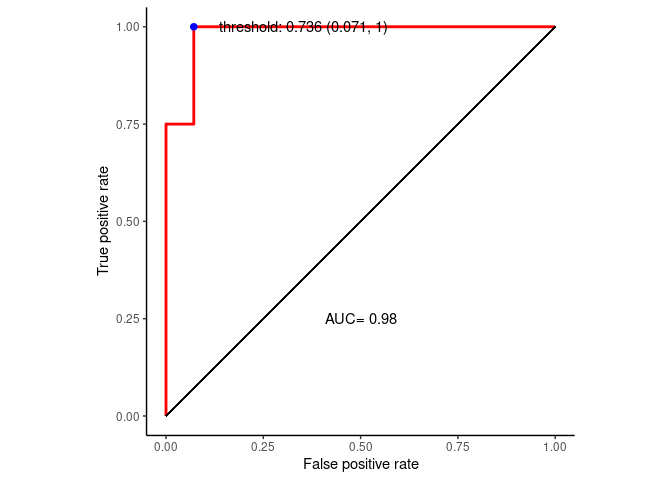

基于默认阈值绘制混淆矩阵并评估模型预测准确度显著性,结果是不显著P-Value [Acc > NIR]>0.05。

# 获得模型结果评估矩阵(`confusion matrix`)

predictions <- predict(borutaConfirmed_rf_default, newdata=test_data)
confusionMatrix(predictions, test_data_group)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction DLBCL FL
##      DLBCL    14  1
##      FL        0  3
##                                           
##                Accuracy : 0.9444          
##                  95% CI : (0.7271, 0.9986)
##     No Information Rate : 0.7778          
##     P-Value [Acc > NIR] : 0.06665         
##                                           
##                   Kappa : 0.8235          
##                                           
##  Mcnemar's Test P-Value : 1.00000         
##                                           
##             Sensitivity : 1.0000          
##             Specificity : 0.7500          
##          Pos Pred Value : 0.9333          
##          Neg Pred Value : 1.0000          
##              Prevalence : 0.7778          
##          Detection Rate : 0.7778          
##    Detection Prevalence : 0.8333          
##       Balanced Accuracy : 0.8750          
##                                           
##        'Positive' Class : DLBCL           
## 

基于选定的最优阈值制作混淆矩阵并评估模型预测准确度显著性,结果是不显著P-Value [Acc > NIR]>0.05。

predict_result <- data.frame(Predict_status=c(T,F), Predict_class=colnames(prediction_prob))

head(predict_result)

##   Predict_status Predict_class
## 1           TRUE         DLBCL
## 2          FALSE            FL

predictions2 <- plyr::join(data.frame(Predict_status=prediction_prob[,1] > best_thresh[1,1]), predict_result)

predictions2 <- as.factor(predictions2$Predict_class)

confusionMatrix(predictions2, test_data_group)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction DLBCL FL
##      DLBCL    13  0
##      FL        1  4
##                                           
##                Accuracy : 0.9444          
##                  95% CI : (0.7271, 0.9986)
##     No Information Rate : 0.7778          
##     P-Value [Acc > NIR] : 0.06665         
##                                           
##                   Kappa : 0.8525          
##                                           
##  Mcnemar's Test P-Value : 1.00000         
##                                           
##             Sensitivity : 0.9286          
##             Specificity : 1.0000          
##          Pos Pred Value : 1.0000          
##          Neg Pred Value : 0.8000          
##              Prevalence : 0.7778          
##          Detection Rate : 0.7222          
##    Detection Prevalence : 0.7222          
##       Balanced Accuracy : 0.9643          
##                                           
##        'Positive' Class : DLBCL           
## 

使用 Caret 进行调参和建模时换一种评估方式，从评估准确性变为评估ROC值，获得的mtry值是一样的，都是1。

library(caret)
# Create model with default parameters
trControl <- trainControl(method="repeatedcv", number=10, repeats=5,
                          summaryFunction=twoClassSummary, classProbs = TRUE)

# train model
if(file.exists('rda/borutaConfirmed_rf_roc.rda')){
   borutaConfirmed_rf_roc <- readRDS("rda/borutaConfirmed_rf_roc.rda")
} else {
  # 设置随机数种子，使得结果可重复
  seed <- 2
  set.seed(seed)
  # 根据经验或感觉设置一些待查询的参数和参数值
  tuneGrid <- expand.grid(mtry=boruta_mtry)
  
  borutaConfirmed_rf_roc <- train(x=boruta_train_data, y=train_data_group, method="rf", 
                     tuneGrid = tuneGrid, # 
                     metric="ROC", #metric='Kappa'
                     trControl=trControl)
  saveRDS(borutaConfirmed_rf_roc, "rda/borutaConfirmed_rf_roc.rda")
}
print(borutaConfirmed_rf_roc)

## Random Forest 
## 
## 59 samples
## 56 predictors
##  2 classes: 'DLBCL', 'FL' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 5 times) 
## Summary of sample sizes: 53, 52, 54, 53, 52, 53, ... 
## Resampling results across tuning parameters:
## 
##   mtry  ROC     Sens   Spec
##    1    0.9980  0.977  0.99
##    2    0.9955  0.977  0.92
##    3    0.9935  0.977  0.87
##    4    0.9955  0.977  0.87
##    5    0.9935  0.982  0.85
##    6    0.9935  0.973  0.85
##    7    0.9935  0.977  0.85
##    8    0.9915  0.973  0.85
##    9    0.9935  0.973  0.85
##   10    0.9915  0.973  0.83
##   16    0.9890  0.973  0.83
##   25    0.9800  0.965  0.83
##   36    0.9800  0.965  0.81
##   49    0.9680  0.961  0.81
## 
## ROC was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 1.

采用默认mtry值或配合降低tree的数目，都不能改善预测准确度。

if(file.exists('rda/borutaConfirmed_rf_mtry_default.rda')){
  borutaConfirmed_rf_mtry_default <- readRDS("rda/borutaConfirmed_rf_mtry_default.rda")
} else {
  # method="none" 不再抽样，用全部数据训练模型
  trControl <- trainControl(method="none", classProbs = T)

  # 设置随机数种子，使得结果可重复
  seed <- 1
  set.seed(seed)

  borutaConfirmed_rf_mtry_default <- train(x=boruta_train_data, 
                                           y=train_data_group, method="rf", 
                    # 用默认mtry值
                    tuneGrid = expand.grid(mtry=sqrt(length(boruta.confirmed))),
                    trControl=trControl, ntree=300)
  saveRDS(borutaConfirmed_rf_mtry_default, "rda/borutaConfirmed_rf_mtry_default.rda")
}

print(borutaConfirmed_rf_mtry_default)

## Random Forest 
## 
## 59 samples
## 56 predictors
##  2 classes: 'DLBCL', 'FL' 
## 
## No pre-processing
## Resampling: None

predictions <- predict(borutaConfirmed_rf_mtry_default, newdata=test_data)
confusionMatrix(predictions, test_data_group)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction DLBCL FL
##      DLBCL    14  2
##      FL        0  2
##                                           
##                Accuracy : 0.8889          
##                  95% CI : (0.6529, 0.9862)
##     No Information Rate : 0.7778          
##     P-Value [Acc > NIR] : 0.2022          
##                                           
##                   Kappa : 0.6087          
##                                           
##  Mcnemar's Test P-Value : 0.4795          
##                                           
##             Sensitivity : 1.0000          
##             Specificity : 0.5000          
##          Pos Pred Value : 0.8750          
##          Neg Pred Value : 1.0000          
##              Prevalence : 0.7778          
##          Detection Rate : 0.7778          
##    Detection Prevalence : 0.8889          
##       Balanced Accuracy : 0.7500          
##                                           
##        'Positive' Class : DLBCL           
## 

5.2.3.2 Boruta 选择的所有可能有贡献的变量拟合模型

选择关键特征变量和可能是关键特征变量的变量相关的数据。对这套数据集结果并没有变好。

# withTentative=T: 包含tentative变量
boruta.confirmed <- getSelectedAttributes(boruta, withTentative = T)

# 提取训练集的特征变量子集
boruta_train_data <- train_data[, boruta.confirmed]
boruta_mtry <- generateTestVariableSet(length(boruta.confirmed))

library(caret)
# Create model with default parameters
trControl <- trainControl(method="repeatedcv", number=10, repeats=5)

# train model
if(file.exists('rda/borutaConfirmedTentative_rf_default.rda')){
   borutaConfirmedTentative_rf_default <- readRDS("rda/borutaConfirmedTentative_rf_default.rda")
} else {
  # 设置随机数种子，使得结果可重复
  seed <- 1
  set.seed(seed)
  # 根据经验或感觉设置一些待查询的参数和参数值
  tuneGrid <- expand.grid(mtry=boruta_mtry)
  
  borutaConfirmedTentative_rf_default <- train(x=boruta_train_data, y=train_data_group, method="rf", 
                     tuneGrid = tuneGrid, # 
                     metric="Accuracy", #metric='Kappa'
                     trControl=trControl)
  saveRDS(borutaConfirmedTentative_rf_default, "rda/borutaConfirmedTentative_rf_default.rda")
}

# 获得模型结果评估矩阵(`confusion matrix`)

predictions <- predict(borutaConfirmedTentative_rf_default, newdata=test_data)
confusionMatrix(predictions, test_data_group)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction DLBCL FL
##      DLBCL    14  2
##      FL        0  2
##                                           
##                Accuracy : 0.8889          
##                  95% CI : (0.6529, 0.9862)
##     No Information Rate : 0.7778          
##     P-Value [Acc > NIR] : 0.2022          
##                                           
##                   Kappa : 0.6087          
##                                           
##  Mcnemar's Test P-Value : 0.4795          
##                                           
##             Sensitivity : 1.0000          
##             Specificity : 0.5000          
##          Pos Pred Value : 0.8750          
##          Neg Pred Value : 1.0000          
##              Prevalence : 0.7778          
##          Detection Rate : 0.7778          
##    Detection Prevalence : 0.8889          
##       Balanced Accuracy : 0.7500          
##                                           
##        'Positive' Class : DLBCL           
## 

borutaConfirmedTentative_rf_default

## Random Forest 
## 
## 59 samples
## 89 predictors
##  2 classes: 'DLBCL', 'FL' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 5 times) 
## Summary of sample sizes: 53, 53, 54, 53, 53, 54, ... 
## Resampling results across tuning parameters:
## 
##   mtry  Accuracy   Kappa    
##    1    0.9876190  0.9725880
##    2    0.9809524  0.9573499
##    3    0.9712381  0.9214397
##    4    0.9565714  0.8526301
##    5    0.9492381  0.8242968
##    6    0.9492381  0.8242968
##    7    0.9532381  0.8442968
##    8    0.9492381  0.8242968
##    9    0.9492381  0.8242968
##   10    0.9492381  0.8242968
##   16    0.9492381  0.8242968
##   25    0.9425714  0.8042968
##   36    0.9425714  0.8042968
##   49    0.9397143  0.7960615
##   64    0.9459048  0.8109635
##   81    0.9340000  0.7795909
## 
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 1.

5.2.4 Boruta算法的注意事项

1. 在运行Boruta算法前确保缺失值和空值都已被填充。
2. Boruta不排除共线性变量。如果构建模型时需要排除共线性变量，需要再次处理。
3. 计算速度相对慢。

5.3 特征递归消除(RFE, recursive feature elimination)

5.3.1 RFE算法理论概述

RFE 算法通过增加或移除特定特征变量获得能最大化模型性能的最优组合变量。

5.3.2 RFE基本算法

1. 使用所有特征变量训练模型
2. 计算每个特征变量的重要性并进行排序
3. 对每一个变量子集 \(S_{i}, i=1...S\):
   1. 提取前\(S_{i}\)个最重要的特征变量
   2. 基于新数据集训练模型
   3. 重计算每个特征变量的重要性并进行排序（可选）
4. 计算比较每个子集获得的模型的效果
5. 决定最优的特征变量集合
6. 选择最优变量集合的模型为最终模型

注：每次筛选子集特征变量构建模型时是否对变量在进行重新排序和选择是可选的。之前有评估表示对随机森林模型不建议每次都计算变量重要性，这会降低最终的性能。对基于高度共线性变量构建的线性模型，每一次重新计算变量重要性可以略微提高模型性能。

在使用RFE算法时需要注意过拟合问题。假如在一个很大数目的无意义特征变量组成的数据集中有一个变量正好与分类结果完全吻合。RFE算法将会给这个变量很好的重要性得分和排序，包括这个变量的模型在构建评估时错误率也较低。需要一个独立的测试集或验证集才能发现这个被选出的特征变量是无意义的。这也被称为选择偏好 (selection bias)。

在当前的 RFE 算法中，训练集被至少用于 3 个目的：特征变量筛选、模型拟合和性能评估。单一的静态训练集不能满足这些需求，除非训练集中的样品特别多（尤其是显著多于变量数目）。

为了更好地评估特征选择过程中的性能波动，需要在前述算法的外层再增加一层重抽样过程（如10-折交叉验证）。这可以提供很好地性能评估，但也增加了很多计算压力，建议使用并行计算加快速度。

5.3.3 交叉验证RFE算法

1. 对每一次重采样迭代
   1. 把训练集拆分为新训练集和验证集
   2. 采用新训练集和所有特征变量训练模型
   3. 使用验证集评估模型
   4. 计算所有特征变量重要性并进行排序
   5. 对每一个变量子集 \(S_{i}, i=1...S\):
      1. 提取前\(S_{i}\)个最重要的特征变量
      2. 基于新数据集训练模型
      3. 采用验证集评估模型
      4. 重计算每个特征变量的重要性并进行排序（可选）
2. 决定合适数目的特征变量
3. 估计用于最终模型构建的特征变量集合
4. 选择最优变量集合采用全部训练集构建最终模型

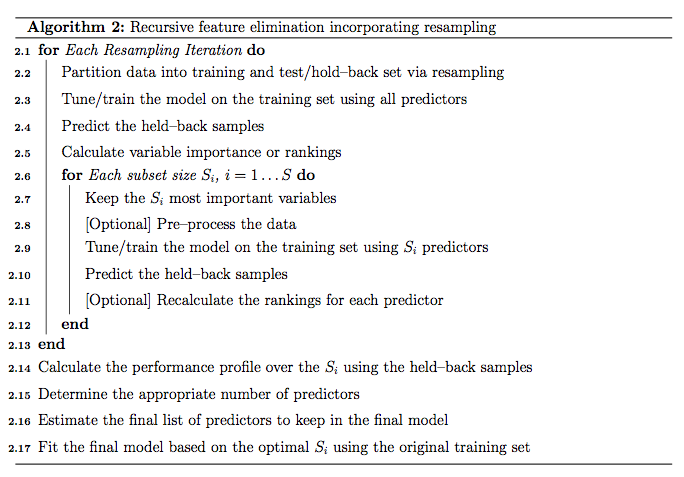
在caret中rfe使用的是第二种算法。

5.3.4 RFE算法实战

rfe函数有 4 个关键参数：

• x: 训练集数值矩阵 (不包含响应值或分类信息)
• y: 响应值或分类信息向量
• sizes: 一个整数向量，设定需要评估的变量子集的大小。默认是2^(2:4)。
• rfeControl: 模型评估所用的方法、性能指标和排序方式等。

一些模型有预定义的函数集可供使用，如linear regression (lmFuncs), random forests (rfFuncs), naive Bayes (nbFuncs), bagged trees (treebagFuncs)和其它可用于train函数的函数集。

# 因运行时间长，故存储起运行结果供后续测试
library(caret)
if(file.exists('rda/rfe_rffuncs.rda')){
  rfe <- readRDS("rda/rfe_rffuncs.rda")
} else {
  subsets <- generateTestVariableSet(ncol(train_data))
  # rfFuncs
  control <- rfeControl(functions=rfFuncs, method="repeatedcv", number=10, repeats=5)

  rfe <- rfe(x=train_data, y=train_data_group, size=subsets, rfeControl=control)
  saveRDS(rfe, "rda/rfe_rffuncs.rda")
}

print(rfe, top=10)

## 
## Recursive feature selection
## 
## Outer resampling method: Cross-Validated (10 fold, repeated 5 times) 
## 
## Resampling performance over subset size:
## 
##  Variables Accuracy  Kappa AccuracySD KappaSD Selected
##          1   0.7152 0.2585     0.1740  0.3743         
##          2   0.7990 0.4464     0.1595  0.4398         
##          3   0.8341 0.5143     0.1342  0.4096         
##          4   0.8387 0.5266     0.1362  0.4231         
##          5   0.8678 0.6253     0.1359  0.4080         
##          6   0.8937 0.6790     0.1285  0.4095         
##          7   0.8906 0.6796     0.1320  0.4031         
##          8   0.8995 0.6939     0.1175  0.3904         
##          9   0.8803 0.6343     0.1309  0.4234         
##         10   0.9017 0.7036     0.1186  0.3847         
##         16   0.9250 0.7781     0.1066  0.3398         
##         25   0.9223 0.7663     0.1151  0.3632         
##         27   0.9318 0.7927     0.1094  0.3483         
##         36   0.9356 0.7961     0.1123  0.3657         
##         49   0.9323 0.7895     0.1128  0.3649         
##         64   0.9356 0.8076     0.1123  0.3488         
##         81   0.9385 0.8193     0.1083  0.3305         
##        100   0.9356 0.8076     0.1123  0.3488         
##        125   0.9356 0.8095     0.1123  0.3478         
##        216   0.9394 0.8129     0.1149  0.3650        *
##        256   0.9361 0.8044     0.1155  0.3656         
##        343   0.9219 0.7516     0.1247  0.4062         
##        512   0.9288 0.7799     0.1239  0.3933         
##        625   0.9266 0.7790     0.1165  0.3658         
##        729   0.9252 0.7567     0.1278  0.4211         
##       1000   0.9259 0.7681     0.1272  0.4077         
##       1296   0.9181 0.7313     0.1250  0.4183         
##       2401   0.8787 0.5666     0.1285  0.4639         
##       4096   0.8787 0.5701     0.1252  0.4525         
##       6561   0.8521 0.4619     0.1221  0.4510         
##       7070   0.8623 0.4987     0.1268  0.4635         
## 
## The top 10 variables (out of 216):
##    HG4074.HT4344_at, D55716_at, U63743_at, M63835_at, L42324_at, X02152_at, D31887_at, D82348_at, X17620_at, U56102_at

绘制下模型的准确性随选择的重要性变量的数目的变化

plot(rfe, type=c("g", "o"))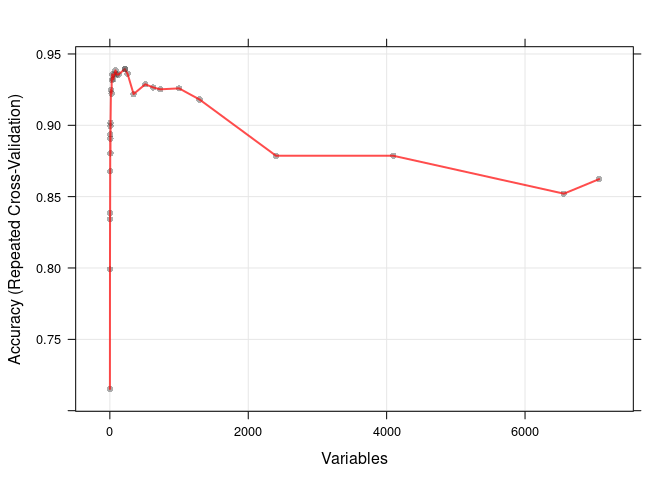

可以使用predictors函数提取最终选定的最小关键特征变量集，也可以直接从rfe对象中提取。

predictors(rfe)

##   [1] "HG4074.HT4344_at"   "D55716_at"          "U63743_at"         
##   [4] "M63835_at"          "L42324_at"          "X02152_at"         
##   [7] "D31887_at"          "D82348_at"          "X17620_at"         
##  [10] "U56102_at"          "L17131_rna1_at"     "U14518_at"         
##  [13] "U16307_at"          "X56494_at"          "Z11793_at"         
##  [16] "Z21966_at"          "X91911_s_at"        "D13633_at"         
##  [19] "M14328_s_at"        "J03909_at"          "U68030_at"         
##  [22] "U38896_at"          "U59309_at"          "HG1980.HT2023_at"  
##  [25] "D87119_at"          "X62078_at"          "HG3928.HT4198_at"  
##  [28] "AC002073_cds1_at"   "M57710_at"          "U37426_at"         
##  [31] "X16983_at"          "V00594_s_at"        "X01060_at"         
##  [34] "U47414_at"          "M25753_at"          "X67155_at"         
##  [37] "HG2874.HT3018_at"   "S62696_s_at"        "X03689_s_at"       
##  [40] "U37352_at"          "M63138_at"          "X69433_at"         
##  [43] "X64177_f_at"        "U28386_at"          "X14850_at"         
##  [46] "U23143_at"          "K02268_at"          "Z96810_at"         
##  [49] "J02645_at"          "HG417.HT417_s_at"   "X67951_at"         
##  [52] "X76534_at"          "X65965_s_at"        "D31886_at"         
##  [55] "L27071_at"          "U24169_at"          "X07619_s_at"       
##  [58] "X17567_s_at"        "U24577_at"          "D78134_at"         
##  [61] "L33842_rna1_at"     "U12595_at"          "M20471_at"         
##  [64] "U89942_at"          "D79997_at"          "U09587_at"         
##  [67] "U72935_cds3_s_at"   "M86699_at"          "U03398_at"         
##  [70] "L04510_at"          "M35878_at"          "D16815_at"         
##  [73] "L42621_at"          "L19437_at"          "U74612_at"         
##  [76] "U81375_at"          "Z26634_at"          "D43950_at"         
##  [79] "M94880_f_at"        "U43189_s_at"        "X68560_at"         
##  [82] "U79295_at"          "HG4258.HT4528_at"   "U78525_at"         
##  [85] "L04282_at"          "M37815_cds1_at"     "U73379_at"         
##  [88] "L06419_at"          "M74093_at"          "X16396_at"         
##  [91] "Z49269_at"          "X53961_at"          "D38048_at"         
##  [94] "U46006_s_at"        "L02426_at"          "HG2279.HT2375_at"  
##  [97] "Z50115_s_at"        "HG3934.HT4204_at"   "M94556_at"         
## [100] "D26599_at"          "V00594_at"          "X59543_at"         
## [103] "X59834_at"          "M60830_at"          "HG110.HT110_s_at"  
## [106] "L00022_s_at"        "M65290_at"          "M86737_at"         
## [109] "X74801_at"          "L06132_at"          "U96113_at"         
## [112] "Y08374_rna1_at"     "M13792_at"          "Z30644_at"         
## [115] "HG4541.HT4946_s_at" "X12530_s_at"        "U29680_at"         
## [118] "X86098_at"          "S73591_at"          "U67932_s_at"       
## [121] "M10901_at"          "L25876_at"          "U14528_at"         
## [124] "L36720_at"          "X12447_at"          "J04173_at"         
## [127] "J04988_at"          "L19686_rna1_at"     "L11066_at"         
## [130] "X00437_s_at"        "X60003_s_at"        "M22760_at"         
## [133] "D83597_at"          "X81836_s_at"        "M12529_at"         
## [136] "D49824_s_at"        "X03066_at"          "L23808_at"         
## [139] "D25328_at"          "X51408_at"          "M22382_at"         
## [142] "D84361_at"          "D38073_at"          "M34338_s_at"       
## [145] "HG1153.HT1153_at"   "L19314_at"          "X74794_at"         
## [148] "M95724_at"          "M83751_at"          "Y09615_at"         
## [151] "U18383_s_at"        "U05340_at"          "U40369_rna1_at"    
## [154] "Z35227_at"          "U00238_rna1_at"     "X67235_s_at"       
## [157] "X52425_at"          "Z69915_at"          "U43522_at"         
## [160] "M26004_s_at"        "U77949_at"          "AB002409_at"       
## [163] "X59244_f_at"        "M21259_at"          "U37122_at"         
## [166] "U22055_at"          "M80335_at"          "M92843_s_at"       
## [169] "U06698_at"          "X54942_at"          "M22960_at"         
## [172] "K02574_at"          "X52851_rna1_at"     "X53793_at"         
## [175] "M95623_cds1_at"     "U15008_at"          "U89922_s_at"       
## [178] "X60787_s_at"        "X06956_at"          "Y00705_at"         
## [181] "U50535_at"          "U21931_at"          "X82207_at"         
## [184] "U03858_at"          "U07550_at"          "M87339_at"         
## [187] "U15642_s_at"        "J02960_cds1_s_at"   "M61764_at"         
## [190] "L19183_at"          "L10717_at"          "D13118_at"         
## [193] "X86400_at"          "Z14244_at"          "X77922_s_at"       
## [196] "K03430_at"          "D45248_at"          "M31642_at"         
## [199] "X15183_at"          "K01396_at"          "X05345_at"         
## [202] "M36803_at"          "M34181_at"          "M15059_at"         
## [205] "L29306_s_at"        "U18321_at"          "U61262_at"         
## [208] "L33930_s_at"        "D90070_s_at"        "Z49254_at"         
## [211] "U30872_at"          "Y09392_s_at"        "U21090_at"         
## [214] "U17032_at"          "D00763_at"          "HG3075.HT3236_s_at"

存储起来用于跟Boruta鉴定出的特征变量比较

caretRfe_variables <- data.frame(Item=rfe$optVariables, Type="Caret_RFE")

5.3.4.1 比较Boruta与RFE筛选出的特征变量的异同

vairables <- rbind(boruta.finalVars, boruta.finalVarsWithTentative, caretRfe_variables)
library(VennDiagram)
library(ImageGP)
sp_vennDiagram2(vairables, item_variable = "Item", set_variable = "Type", manual_color_vector ="Set1")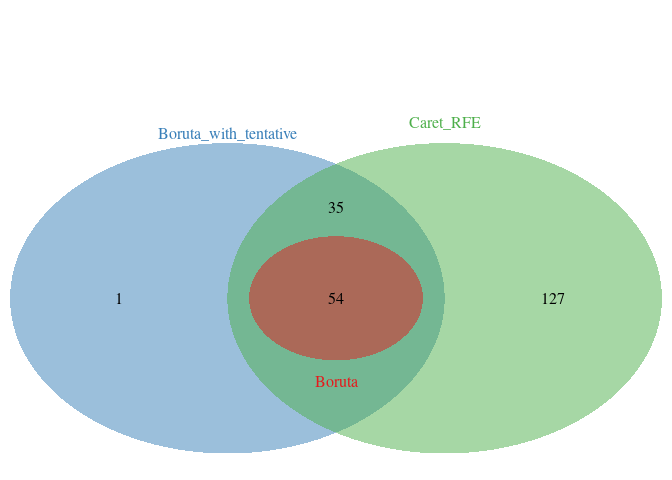

5.3.4.2 评估RFE变量筛选过程中构建的最终模型的效果

最终拟合的模型可通过rfe$fit获取，用于后续预测分析。

library(randomForest)
rfe$fit

## 
## Call:
##  randomForest(x = x, y = y, importance = TRUE) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 14
## 
##         OOB estimate of  error rate: 5.08%
## Confusion matrix:
##       DLBCL FL class.error
## DLBCL    43  1  0.02272727
## FL        2 13  0.13333333

但此模型没有进行调参。虽然用的变量多了，但预测效果没有比Boruta筛选的特征变量结果好。P-Value [Acc > NIR] : 0.2022不显著。

# 获得模型结果评估矩阵(`confusion matrix`)

predictions <- predict(rfe$fit, newdata=test_data)
confusionMatrix(predictions, test_data_group)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction DLBCL FL
##      DLBCL    14  2
##      FL        0  2
##                                           
##                Accuracy : 0.8889          
##                  95% CI : (0.6529, 0.9862)
##     No Information Rate : 0.7778          
##     P-Value [Acc > NIR] : 0.2022          
##                                           
##                   Kappa : 0.6087          
##                                           
##  Mcnemar's Test P-Value : 0.4795          
##                                           
##             Sensitivity : 1.0000          
##             Specificity : 0.5000          
##          Pos Pred Value : 0.8750          
##          Neg Pred Value : 1.0000          
##              Prevalence : 0.7778          
##          Detection Rate : 0.7778          
##    Detection Prevalence : 0.8889          
##       Balanced Accuracy : 0.7500          
##                                           
##        'Positive' Class : DLBCL           
## 

5.3.4.3 基于RFE选择的特征变量再次调参构建模型

# 提取训练集的特征变量子集
rfe_train_data <- train_data[, caretRfe_variables$Item]
rfe_mtry <- generateTestVariableSet(length(caretRfe_variables$Item))

使用 Caret 进行调参和建模

library(caret)
# Create model with default parameters
trControl <- trainControl(method="repeatedcv", number=10, repeats=5)

# train model
if(file.exists('rda/rfeVariable_rf_default.rda')){
   rfeVariable_rf_default <- readRDS("rda/rfeVariable_rf_default.rda")
} else {
  # 设置随机数种子，使得结果可重复
  seed <- 1
  set.seed(seed)
  # 根据经验或感觉设置一些待查询的参数和参数值
  tuneGrid <- expand.grid(mtry=rfe_mtry)
  
  rfeVariable_rf_default <- train(x=rfe_train_data, y=train_data_group, method="rf", 
                     tuneGrid = tuneGrid, # 
                     metric="Accuracy", #metric='Kappa'
                     trControl=trControl)
  saveRDS(rfeVariable_rf_default, "rda/rfeVariable_rf_default.rda")
}
print(rfeVariable_rf_default)

## Random Forest 
## 
##  59 samples
## 216 predictors
##   2 classes: 'DLBCL', 'FL' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 5 times) 
## Summary of sample sizes: 53, 53, 54, 53, 53, 54, ... 
## Resampling results across tuning parameters:
## 
##   mtry  Accuracy   Kappa    
##     1   0.9802857  0.9459213
##     2   0.9707619  0.9091146
##     3   0.9600952  0.8725321
##     4   0.9554286  0.8405432
##     5   0.9599048  0.8612016
##     6   0.9525714  0.8326301
##     7   0.9572381  0.8642968
##     8   0.9492381  0.8242968
##     9   0.9492381  0.8242968
##    10   0.9492381  0.8242968
##    16   0.9492381  0.8242968
##    25   0.9492381  0.8242968
##    27   0.9463810  0.8160615
##    36   0.9492381  0.8242968
##    49   0.9492381  0.8242968
##    64   0.9425714  0.8042968
##    81   0.9363810  0.7874901
##   100   0.9397143  0.7960615
##   125   0.9311429  0.7713556
## 
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 1.

结果还是不显著P-Value [Acc > NIR]>0.05。效果弱于Boruta筛选出的特征变量构建的模型。

# 获得模型结果评估矩阵(`confusion matrix`)

predictions <- predict(rfeVariable_rf_default, newdata=test_data)
confusionMatrix(predictions, test_data_group)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction DLBCL FL
##      DLBCL    14  2
##      FL        0  2
##                                           
##                Accuracy : 0.8889          
##                  95% CI : (0.6529, 0.9862)
##     No Information Rate : 0.7778          
##     P-Value [Acc > NIR] : 0.2022          
##                                           
##                   Kappa : 0.6087          
##                                           
##  Mcnemar's Test P-Value : 0.4795          
##                                           
##             Sensitivity : 1.0000          
##             Specificity : 0.5000          
##          Pos Pred Value : 0.8750          
##          Neg Pred Value : 1.0000          
##              Prevalence : 0.7778          
##          Detection Rate : 0.7778          
##    Detection Prevalence : 0.8889          
##       Balanced Accuracy : 0.7500          
##                                           
##        'Positive' Class : DLBCL           
## 

5.3.5 使用treebagFuncs运行RFE特征选择

library(ipred)
if(file.exists('rda/rfeTreeBag.rda')){
  rfeTreeBag <- readRDS("rda/rfeTreeBag.rda")
} else {
  subsets <- generateTestVariableSet(ncol(train_data))
  # treebagFuncs
  controlTreeBag <- rfeControl(functions=treebagFuncs, method="repeatedcv", number=10, repeats=5, verbose=T)
  rfeTreeBag <- rfe(x=train_data, y=train_data_group, size=subsets, rfeControl=controlTreeBag)
  saveRDS(rfeTreeBag, "rda/rfeTreeBag.rda")
}

print(rfeTreeBag, top=10)

caretrfeTreeBag_variables <- data.frame(Item=rfeTreeBag$optVariables, Type="Caret_rfeTreeBag")

用 Venn 图绘制下三种算法计算出的相关变量的异同。

vairables <- rbind(boruta.finalVars, caretRfe_variables, caretrfeTreeBag_variables)
library(VennDiagram)
sp_vennDiagram2(vairables, item_variable = "Item", set_variable = "Type")

5.4 遗传算法 (Genetic algorithms)鉴定特征变量

特征变量的鉴定问题是一个搜索问题。遗传算法模拟达尔文的自然选择。

首先构建一个遗传群体。其中每个个体为不同特征变量组合训练的模型。性能较优的个体之间进行杂交（变量组合）并加以随机突变（变量随机替换）获得新的子代，继续训练模型和评估性能。

# 太慢了，运行了1周未运行完
library(ipred)
if(file.exists('rda/rf_ga.rda')){
  rf_ga <- readRDS("rda/rf_ga.rda")
} else {
  ga_ctrl <- gafsControl(functions=rfGA, method="repeatedcv", number=10, repeats=5, verbose = T)
  rf_ga <- gafs(x=train_data, y=train_data_group, iters=200, gafsControl=ga_ctrl)
  saveRDS(rf_ga, "rda/rf_ga.rda")
}

print(rf_ga, top=10)

5.5 RFE 模拟退火算法

模拟退火算法也是一种全局搜索算法。通过对起始特征变量进行随机置换选择获得最优的组合。

耗时 3.38 小时rf_sa$times$everything[1]。

if(file.exists('rda/rf_sa.rda')){
  rf_sa <- readRDS("rda/rf_sa.rda")
} else {
  sa_ctrl <- safsControl(functions=rfSA, method="repeatedcv", number=10, repeats=5, verbose = T)
  rf_sa <- safs(x=train_data, y=train_data_group, iters=250, safsControl=sa_ctrl)
  saveRDS(rf_sa, "rda/rf_sa.rda")
}

print(rf_sa, top=10)

## 
## Simulated Annealing Feature Selection
## 
## 59 samples
## 7070 predictors
## 2 classes: 'DLBCL', 'FL' 
## 
## Maximum search iterations: 250 
## 
## Internal performance values: Accuracy, Kappa
## Subset selection driven to maximize internal Accuracy 
## 
## External performance values: Accuracy, Kappa
## Best iteration chose by maximizing external Accuracy 
## External resampling method: Cross-Validated (10 fold, repeated 5 times) 
## 
## During resampling, no variables were selected.
## 
## In the final search using the entire training set:
##    * 1703 features selected at iteration 152 including:
##      AB000114_at ... 
##    * external performance at this iteration is
## 
##    Accuracy       Kappa 
##      0.8587      0.4963

plot(rf_sa)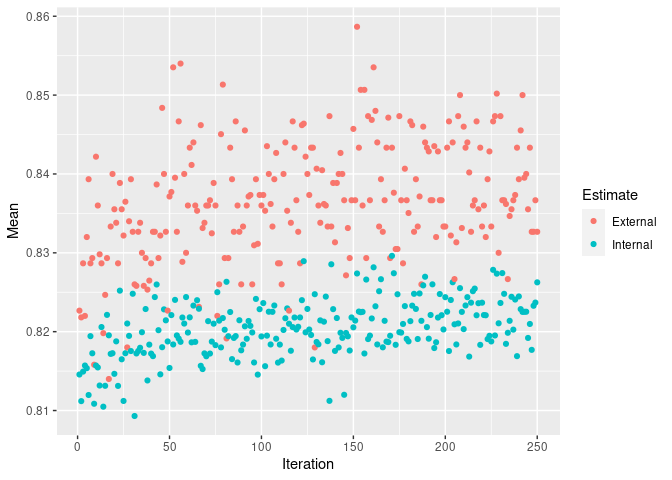

varSelRF

https://rstudio-pubs-static.s3.amazonaws.com/297334_5a1c4687afa04b83a3ca5d0e59db4b46.html

5.5.1 References

• https://stats.stackexchange.com/questions/264360/boruta-all-relevant-feature-selection-vs-random-forest-variables-of-importanc
• https://stats.stackexchange.com/questions/403381/using-random-forest-variable-importance-for-feature-selection?rq=1
• http://no-free-lunch.org/
• Boruta (imputing) https://www.datacamp.com/community/tutorials/feature-selection-R-boruta
• https://cran.r-project.org/web/packages/ipred/vignettes/ipred-examples.pdf
• y一套特征选择、模型比较方案 https://azavea.github.io/building-inspection-prediction/results.html
• Caret RFE https://stats.stackexchange.com/questions/35009/feature-selection-and-parameter-tuning-with-caret-for-random-forest?rq=1
• https://zhuanlan.zhihu.com/p/33730850
• https://datascience-enthusiast.com/R/ML_python_R_part1.html
• 特征提取方法总结 https://stats.stackexchange.com/questions/443234/random-forest-in-r-how-to-perform-feature-extraction-and-reach-the-best-accura
• Evaluation of variable selection methods for random forests and omics data sets https://academic.oup.com/bib/article/20/2/492/4554516
• https://stats.stackexchange.com/questions/259649/random-forest-variable-selection
• Caret RFE https://topepo.github.io/caret/recursive-feature-elimination.html
• Beware Default Random Forest Importances https://explained.ai/rf-importance/index.html
• Boruta paper https://core.ac.uk/download/pdf/6340269.pdf?repositoryId=153
• 很好的生成模拟数据和分类的方式 https://www.cybaea.net/Journal/2010/11/15/Feature-selection-All-relevant-selection-with-the-Boruta-package/
• Caret RFE https://www.cybaea.net/Journal/2010/11/16/Feature-selection-Using-the-caret-package/
• Compare Boruta and Caret https://www.cybaea.net/Journal/2010/11/25/Benchmarking-feature-selection-with-Boruta-and-caret/
• Variable importance https://stats.stackexchange.com/questions/197827/how-to-interpret-mean-decrease-in-accuracy-and-mean-decrease-gini-in-random-fore?rq=1
• permutation variable selection https://academic.oup.com/bioinformatics/article/26/10/1340/193348?login=true
• feature selection https://hal.archives-ouvertes.fr/file/index/docid/755489/filename/PRLv4.pdf
• Boruta application https://www.listendata.com/2017/05/feature-selection-boruta-package.html
• Caret GA https://stackoverflow.com/questions/56826532/carets-feature-selection-using-genetic-algorithms-how-to-extract-the-results
• Python sci-kit-learn 特征选择 https://towardsdatascience.com/feature-selection-using-random-forest-26d7b747597f