6 基于随机森林模型实战机器学习
6.1 随机森林实操
为了展示随机森林的操作,我们用一套早期的前列腺癌和癌旁基因表达芯片数据集,包含102个样品(50个正常,52个肿瘤),2个分组和9021个变量 (基因)。(https://file.biolab.si/biolab/supp/bi-cancer/projections/info/prostata.html)
6.1.1 数据格式和读入数据
输入数据为标准化之后的表达矩阵,基因在行,样本在列。随机森林对数值分布没有假设。每个基因表达值用于分类时是基因内部在不同样品直接比较,只要是样品之间标准化的数据即可,其他任何线性转换如log2,scale等都没有影响。
- 样品表达数据:prostat.expr.txt
- 样品分组信息:prostat.metadata.txt
expr_file <- "data/prostat.expr.symbol.txt"
metadata_file <- "data/prostat.metadata.txt"
# 每个基因表达值是内部比较,只要是样品之间标准化的数据即可,其它什么转换都关系不大
# 机器学习时,字符串还是默认为因子类型的好
expr_mat <- read.table(expr_file, row.names = 1, header = T, sep="\t", stringsAsFactors =T)
# 处理异常的基因名字
rownames(expr_mat) <- make.names(rownames(expr_mat))
metadata <- read.table(metadata_file, row.names=1, header=T, sep="\t", stringsAsFactors =T)
dim(expr_mat)## [1] 9021 102基因表达表示例如下:
expr_mat[1:4,1:5]## normal_1 normal_2 normal_3 normal_4 normal_5
## AADAC 1.3 -1 -7 -4 5
## AAK1 0.4 0 10 11 8
## AAMP -0.4 20 -7 -14 12
## AANAT 143.3 19 397 245 328Metadata表示例如下
head(metadata)## class
## normal_1 normal
## normal_2 normal
## normal_3 normal
## normal_4 normal
## normal_5 normal
## normal_6 normaltable(metadata)## metadata
## normal tumor
## 50 526.1.2 样品筛选和排序
对读入的表达数据进行转置。通常我们是一行一个基因,一列一个样品。在构建模型时,数据通常是反过来的,一列一个基因,一行一个样品。每一列代表一个变量 (variable),每一行代表一个案例 (case)。这样更方便提取每个变量,且易于把模型中的x,y放到一个矩阵中。
样本表和表达表中的样本顺序对齐一致也是需要确保的一个操作。
# 表达数据转置
# 习惯上我们是一行一个基因,一列一个样品
# 做机器学习时,大部分数据都是反过来的,一列一个基因,一行一个样品
# 每一列代表一个变量
expr_mat <- t(expr_mat)
expr_mat_sampleL <- rownames(expr_mat)
metadata_sampleL <- rownames(metadata)
common_sampleL <- intersect(expr_mat_sampleL, metadata_sampleL)
# 保证表达表样品与METAdata样品顺序和数目完全一致
expr_mat <- expr_mat[common_sampleL,,drop=F]
metadata <- metadata[common_sampleL,,drop=F]6.1.3 判断是分类还是回归
前面读数据时已经给定了参数stringsAsFactors =T,这一步可以忽略了。
- 如果group对应的列为数字,转换为数值型 - 做回归
- 如果group对应的列为分组,转换为因子型 - 做分类
# R4.0之后默认读入的不是factor,需要做一个转换
# devtools::install_github("Tong-Chen/ImageGP")
library(ImageGP)
# 此处的class根据需要修改
group = "class"
# 如果group对应的列为数字,转换为数值型 - 做回归
# 如果group对应的列为分组,转换为因子型 - 做分类
if(numCheck(metadata[[group]])){
if (!is.numeric(metadata[[group]])) {
metadata[[group]] <- mixedToFloat(metadata[[group]])
}
} else{
metadata[[group]] <- as.factor(metadata[[group]])
}6.1.4 随机森林初步分析
library(randomForest)
# 查看参数是个好习惯
# 有了前面的基础概述,再看每个参数的含义就明确了很多
# 也知道该怎么调了
# 每个人要解决的问题不同,通常不是别人用什么参数,自己就跟着用什么参数
# 尤其是到下游分析时
# ?randomForest
# 查看源码
# randomForest:::randomForest.default加载包之后,直接分析一下,看到结果再调参。
# 设置随机数种子,具体含义见 https://mp.weixin.qq.com/s/6plxo-E8qCdlzCgN8E90zg
set.seed(304)
# 直接使用默认参数
rf <- randomForest(expr_mat, metadata[[group]])查看下初步结果, 随机森林类型判断为分类,构建了500棵树,每次决策时从随机选择的94个基因中做最优决策 (mtry),OOB估计的错误率是9.8%,挺高的。
分类效果评估矩阵Confusion matrix,显示normal组的分类错误率为0.06,tumor组的分类错误率为0.13。
rf##
## Call:
## randomForest(x = expr_mat, y = metadata[[group]])
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 94
##
## OOB estimate of error rate: 9.8%
## Confusion matrix:
## normal tumor class.error
## normal 47 3 0.0600000
## tumor 7 45 0.13461546.2 随机森林标准操作流程
6.2.1 拆分训练集和测试集
library(caret)
seed <- 1
set.seed(seed)
train_index <- createDataPartition(metadata[[group]], p=0.75, list=F)
train_data <- expr_mat[train_index,]
train_data_group <- metadata[[group]][train_index]
test_data <- expr_mat[-train_index,]
test_data_group <- metadata[[group]][-train_index]dim(train_data)## [1] 77 9021dim(test_data)## [1] 25 90216.2.2 Boruta特征选择鉴定关键分类变量
# install.packages("Boruta")
library(Boruta)
set.seed(1)
boruta <- Boruta(x=train_data, y=train_data_group, pValue=0.01, mcAdj=T,
maxRuns=300)
boruta## Boruta performed 299 iterations in 1.082747 mins.
## 46 attributes confirmed important: ADH5, AGR2, AKR1B1, ANGPT1,
## ANXA2.....ANXA2P1.....ANXA2P3 and 41 more;
## 8943 attributes confirmed unimportant: AADAC, AAK1, AAMP, AANAT, AARS
## and 8938 more;
## 32 tentative attributes left: ALDH2, ATP6V1G1, C16orf45, CDC42BPA,
## COL4A6 and 27 more;查看下变量重要性鉴定结果(实际上面的输出中也已经有体现了),54个重要的变量,36个可能重要的变量 (tentative variable, 重要性得分与最好的影子变量得分无统计差异),6,980个不重要的变量。
table(boruta$finalDecision)##
## Tentative Confirmed Rejected
## 32 46 8943绘制鉴定出的变量的重要性。变量少了可以用默认绘图,变量多时绘制的图看不清,需要自己整理数据绘图。
定义一个函数提取每个变量对应的重要性值。
library(dplyr)
boruta.imp <- function(x){
imp <- reshape2::melt(x$ImpHistory, na.rm=T)[,-1]
colnames(imp) <- c("Variable","Importance")
imp <- imp[is.finite(imp$Importance),]
variableGrp <- data.frame(Variable=names(x$finalDecision),
finalDecision=x$finalDecision)
showGrp <- data.frame(Variable=c("shadowMax", "shadowMean", "shadowMin"),
finalDecision=c("shadowMax", "shadowMean", "shadowMin"))
variableGrp <- rbind(variableGrp, showGrp)
boruta.variable.imp <- merge(imp, variableGrp, all.x=T)
sortedVariable <- boruta.variable.imp %>% group_by(Variable) %>%
summarise(median=median(Importance)) %>% arrange(median)
sortedVariable <- as.vector(sortedVariable$Variable)
boruta.variable.imp$Variable <- factor(boruta.variable.imp$Variable, levels=sortedVariable)
invisible(boruta.variable.imp)
}boruta.variable.imp <- boruta.imp(boruta)
head(boruta.variable.imp)## Variable Importance finalDecision
## 1 AADAC 0 Rejected
## 2 AADAC 0 Rejected
## 3 AADAC 0 Rejected
## 4 AADAC 0 Rejected
## 5 AADAC 0 Rejected
## 6 AADAC 0 Rejected只绘制Confirmed变量。
library(ImageGP)
sp_boxplot(boruta.variable.imp, melted=T, xvariable = "Variable", yvariable = "Importance",
legend_variable = "finalDecision", legend_variable_order = c("shadowMax", "shadowMean", "shadowMin", "Confirmed"),
xtics_angle = 90)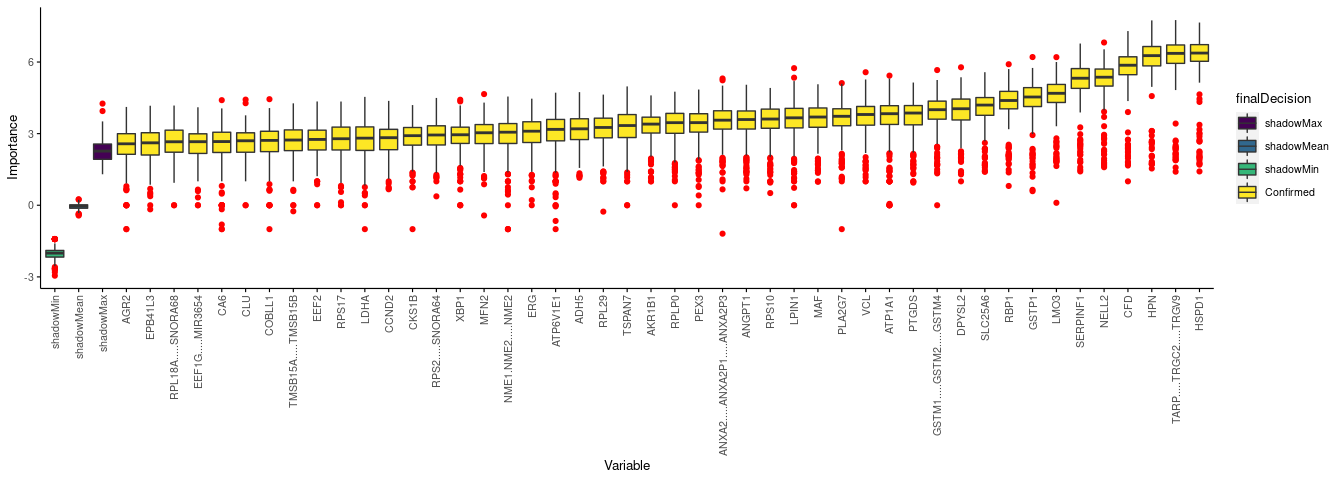
提取重要的变量和可能重要的变量
boruta.finalVarsWithTentative <- data.frame(Item=getSelectedAttributes(boruta, withTentative = T), Type="Boruta_with_tentative")看下这些变量的值的分布
caret::featurePlot(train_data[,boruta.finalVarsWithTentative$Item], train_data_group, plot="box")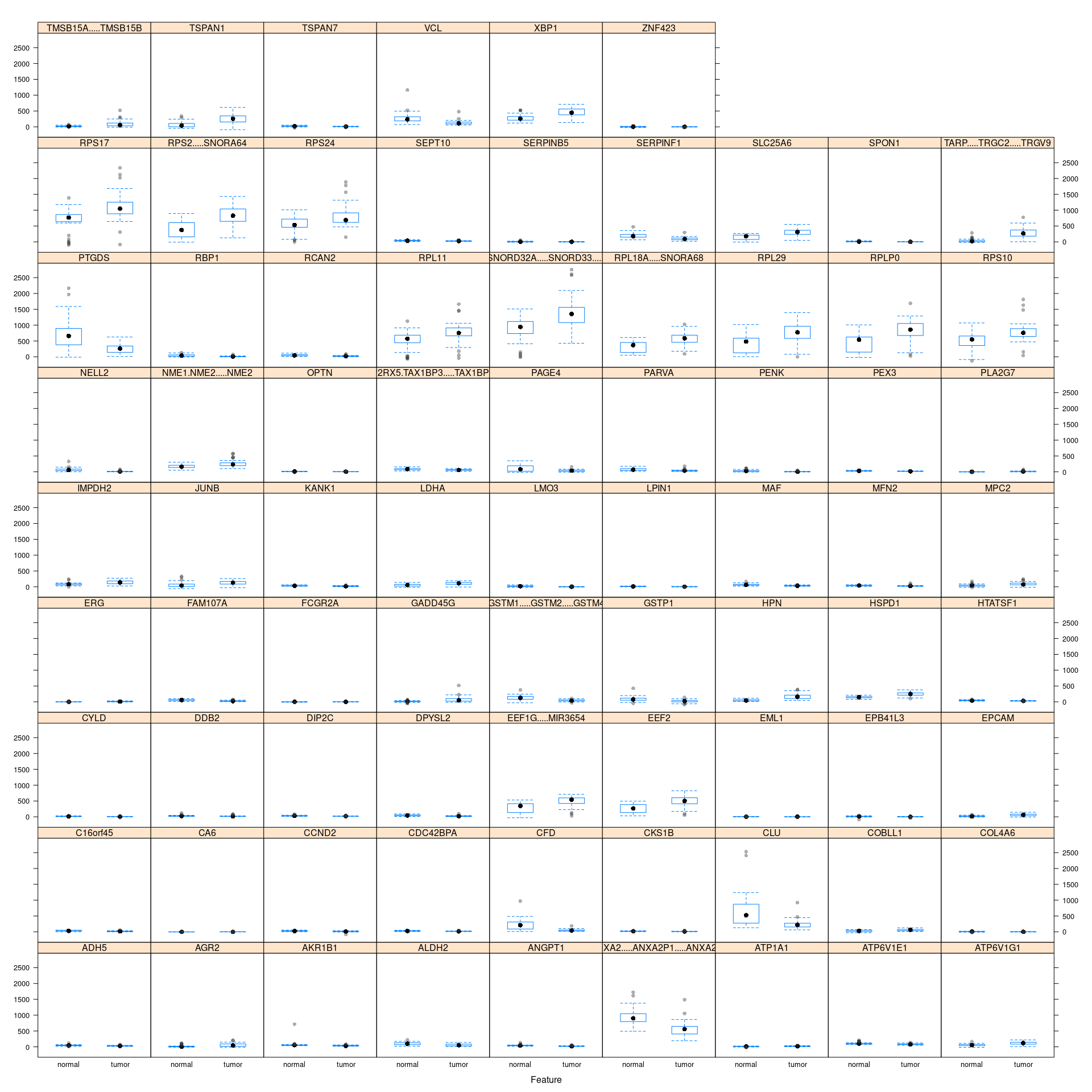
6.2.3 交叉验证选择参数并拟合模型
定义一个函数生成一些列用来测试的mtry (一系列不大于总变量数的数值)。
generateTestVariableSet <- function(num_toal_variable){
max_power <- ceiling(log10(num_toal_variable))
tmp_subset <- c(unlist(sapply(1:max_power, function(x) (1:10)^x, simplify = F)), ceiling(max_power/3))
#return(tmp_subset)
base::unique(sort(tmp_subset[tmp_subset<num_toal_variable]))
}
# generateTestVariableSet(78)选择关键特征变量相关的数据
# 提取训练集的特征变量子集
boruta_train_data <- train_data[, boruta.finalVarsWithTentative$Item]
boruta_mtry <- generateTestVariableSet(ncol(boruta_train_data))使用 Caret 进行调参和建模
library(caret)
# Create model with default parameters
trControl <- trainControl(method="repeatedcv", number=10, repeats=5)
# 根据经验或感觉设置一些待查询的参数和参数值
tuneGrid <- expand.grid(mtry=boruta_mtry)
seed <- 1
set.seed(seed)
borutaConfirmed_rf_default <- train(x=boruta_train_data, y=train_data_group, method="rf",
tuneGrid = tuneGrid, #
metric="Accuracy", #metric='Kappa'
trControl=trControl)
borutaConfirmed_rf_default## Random Forest
##
## 77 samples
## 78 predictors
## 2 classes: 'normal', 'tumor'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 5 times)
## Summary of sample sizes: 71, 69, 69, 69, 69, 69, ...
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa
## 1 0.9352381 0.8708771
## 2 0.9352381 0.8708771
## 3 0.9352381 0.8708771
## 4 0.9377381 0.8758771
## 5 0.9377381 0.8758771
## 6 0.9402381 0.8808771
## 7 0.9402381 0.8808771
## 8 0.9452381 0.8908771
## 9 0.9402381 0.8808771
## 10 0.9452381 0.8908771
## 16 0.9452381 0.8908771
## 25 0.9477381 0.8958771
## 36 0.9452381 0.8908771
## 49 0.9402381 0.8808771
## 64 0.9327381 0.8658771
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 25.绘制准确性随超参的变化曲线
plot(borutaConfirmed_rf_default)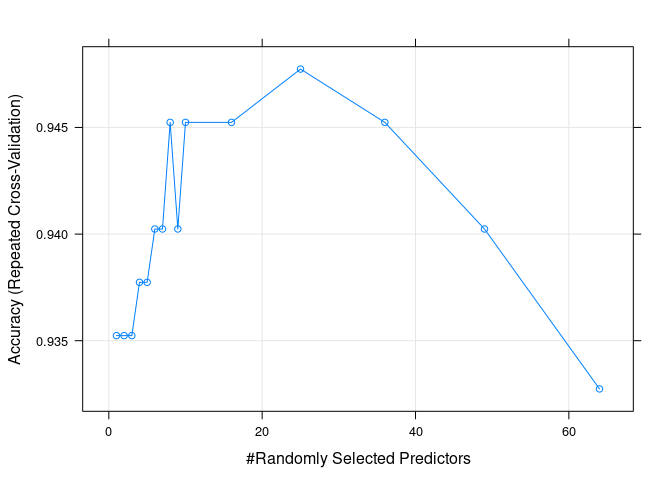
绘制贡献最高的 20 个变量
dotPlot(varImp(borutaConfirmed_rf_default))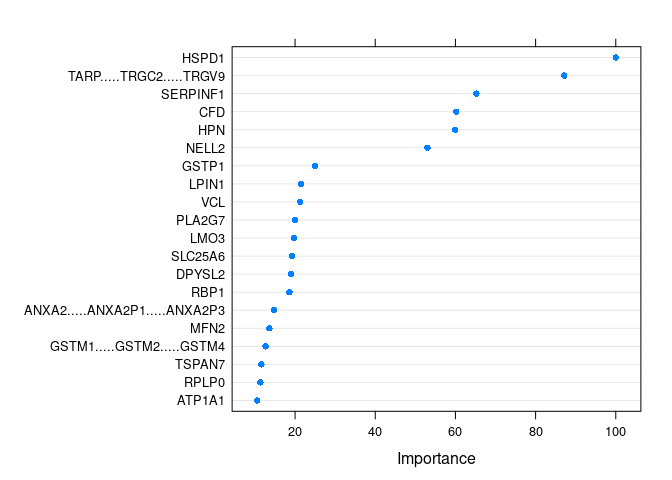
提取最终选择的模型,并绘制 ROC 曲线。(不建议提取finalModel,而是建议直接使用`borutaConfirmed_rf_default)去做后续预测。尤其是训练时指定了数据预处理参数时,使用borutaConfirmed_rf_default会对测试集进行同样的预处理(等同于predict.train),而使用borutaConfirmed_rf_default$finalModel则不会对测试集进行预处理(等同于predict.randomForest)
# Just to clarify this later point a bit further: predict(xx$finalModel, testData) and predict(xx, testData) will be different if one sets the preProcess option when using train.
# On the other hand, when using the finalModel directly it is equivalent using the predict function from the model fitted (predict.randomForest here) instead of predict.train; no pre-proessing takes place.
# borutaConfirmed_rf_default_finalmodel <- borutaConfirmed_rf_default$finalModel采用训练数据集评估构建的模型,Accuracy=1; Kappa=1,非常完美。
模型的预测显著性P-Value [Acc > NIR] : 2.2e-16。其中NIR是No Information Rate,其计算方式为数据集中最大的类包含的数据占总数据集的比例。如某套数据中,分组A有80个样品,分组B有20个样品,我们只要猜A,正确率就会有80%,这就是NIR。如果基于这套数据构建的模型准确率也是80%,那么这个看上去准确率较高的模型也没有意义。confusionMatrix使用binom.test函数检验模型的准确性Accuracy是否显著优于NIR,若P-value<0.05,则表示模型预测准确率显著高于随便猜测。
# 获得模型结果评估矩阵(`confusion matrix`)
predictions_train <- predict(borutaConfirmed_rf_default, newdata=train_data)
confusionMatrix(predictions_train, train_data_group)## Confusion Matrix and Statistics
##
## Reference
## Prediction normal tumor
## normal 38 0
## tumor 0 39
##
## Accuracy : 1
## 95% CI : (0.9532, 1)
## No Information Rate : 0.5065
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 1
##
## Mcnemar's Test P-Value : NA
##
## Sensitivity : 1.0000
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 1.0000
## Prevalence : 0.4935
## Detection Rate : 0.4935
## Detection Prevalence : 0.4935
## Balanced Accuracy : 1.0000
##
## 'Positive' Class : normal
## 绘制ROC曲线,计算模型整体的AUC值,并选择最佳模型。
# 绘制ROC曲线
prediction_prob <- predict(borutaConfirmed_rf_default, newdata=test_data, type="prob")
library(pROC)
roc_curve <- roc(test_data_group, prediction_prob[,1])
roc_curve##
## Call:
## roc.default(response = test_data_group, predictor = prediction_prob[, 1])
##
## Data: prediction_prob[, 1] in 12 controls (test_data_group normal) > 13 cases (test_data_group tumor).
## Area under the curve: 0.9872# roc <- roc(test_data_group, factor(predictions, ordered=T))
# plot(roc)选择最佳阈值
- youden: \(max(sensitivities + r \times specificities)\)
- closest.topleft: \(min((1 - sensitivities)^2 + r \times (1- specificities)^2)\)
r是加权系数,默认是1,其计算方式为\(r = (1 - prevalence) / (cost * prevalence)\).
best.weights控制加权方式:(cost, prevalence)默认是(1, 0.5),据此算出的r为1。
cost: 假阴性率占假阳性率的比例,容忍更高的假阳性率还是假阴性率
prevalence: 关注的类中的个体所占的比例 (
n.cases/(n.controls+n.cases)).
best_thresh <- data.frame(coords(roc=roc_curve, x = "best", input="threshold",
transpose = F, best.method = "youden"))
best_thresh$best <- apply(best_thresh, 1, function (x)
paste0('threshold: ', x[1], ' (', round(1-x[2],3), ", ", round(x[3],3), ")"))
best_thresh## threshold specificity sensitivity best
## 1 0.672 0.9166667 1 threshold: 0.672 (0.083, 1)准备数据绘制ROC曲线
library(ggrepel)
ROC_data <- data.frame(FPR = 1- roc_curve$specificities, TPR=roc_curve$sensitivities)
ROC_data <- ROC_data[with(ROC_data, order(FPR,TPR)),]
p <- ggplot(data=ROC_data, mapping=aes(x=FPR, y=TPR)) +
geom_step(color="red", size=1, direction = "vh") +
geom_segment(aes(x=0, xend=1, y=0, yend=1)) + theme_classic() +
xlab("False positive rate") +
ylab("True positive rate") + coord_fixed(1) + xlim(0,1) + ylim(0,1) +
annotate('text', x=0.5, y=0.25, label=paste('AUC=', round(roc_curve$auc,2))) +
geom_point(data=best_thresh, mapping=aes(x=1-specificity, y=sensitivity), color='blue', size=2) +
geom_text_repel(data=best_thresh, mapping=aes(x=1.05-specificity, y=sensitivity ,label=best))
p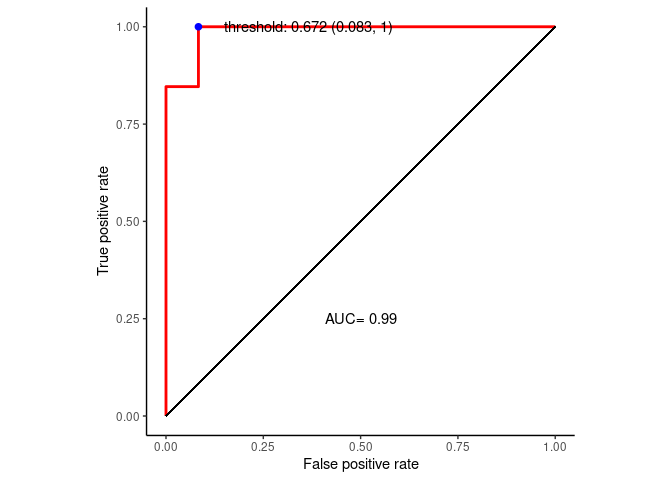
基于选定的最优阈值制作混淆矩阵并评估模型预测准确度显著性,结果是不显著P-Value [Acc > NIR]>0.05。
predict_result <- data.frame(Predict_status=c(T,F), Predict_class=colnames(prediction_prob))
head(predict_result)## Predict_status Predict_class
## 1 TRUE normal
## 2 FALSE tumorpredictions2 <- plyr::join(data.frame(Predict_status=prediction_prob[,1] > best_thresh[1,1]), predict_result)
predictions2 <- as.factor(predictions2$Predict_class)
confusionMatrix(predictions2, test_data_group)## Confusion Matrix and Statistics
##
## Reference
## Prediction normal tumor
## normal 11 0
## tumor 1 13
##
## Accuracy : 0.96
## 95% CI : (0.7965, 0.999)
## No Information Rate : 0.52
## P-Value [Acc > NIR] : 1.913e-06
##
## Kappa : 0.9196
##
## Mcnemar's Test P-Value : 1
##
## Sensitivity : 0.9167
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 0.9286
## Prevalence : 0.4800
## Detection Rate : 0.4400
## Detection Prevalence : 0.4400
## Balanced Accuracy : 0.9583
##
## 'Positive' Class : normal
## 基于默认阈值绘制混淆矩阵并评估模型预测准确度显著性,结果是不显著P-Value [Acc > NIR]>0.05。
# 获得模型结果评估矩阵(`confusion matrix`)
predictions <- predict(borutaConfirmed_rf_default, newdata=test_data)
confusionMatrix(predictions, test_data_group)## Confusion Matrix and Statistics
##
## Reference
## Prediction normal tumor
## normal 12 2
## tumor 0 11
##
## Accuracy : 0.92
## 95% CI : (0.7397, 0.9902)
## No Information Rate : 0.52
## P-Value [Acc > NIR] : 2.222e-05
##
## Kappa : 0.8408
##
## Mcnemar's Test P-Value : 0.4795
##
## Sensitivity : 1.0000
## Specificity : 0.8462
## Pos Pred Value : 0.8571
## Neg Pred Value : 1.0000
## Prevalence : 0.4800
## Detection Rate : 0.4800
## Detection Prevalence : 0.5600
## Balanced Accuracy : 0.9231
##
## 'Positive' Class : normal
##